Procvičování
Procvičování
Lineární rovnice základní
Procvičení k základním lineárním rovnicím – 20 otázek.
Lineární rovnice základní
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičení k základním lineárním rovnicím – 20 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Vyřeš rovnici:
\(y-37=54\)Správně
Špatně
Čísla dáme na jednu stranu, neznámou necháme na druhé. – 37 tedy převedeme zleva doprava, jdeme přes znaménko rovnosti, protose na pravé straně objeví s opačným znaménkem. Čísla sečteme a dostaneme výsledek.
-
Otázka 2 / 20
2. Otázka
Vyřeš rovnici:
\(4u-7=3u+2\)Správně
Špatně
Čísla dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme a máme výsledek.
-
Otázka 3 / 20
3. Otázka
Vyřeš rovnici:
\(18+12y-10=27y+7-13y\)Správně
Špatně
Čísla dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 4 / 20
4. Otázka
Vyřeš rovnici:
\(3y-(y-1)=3\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 5 / 20
5. Otázka
Vyřeš rovnici:
\(3(4u-2)=-2(5-2u)\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 6 / 20
6. Otázka
Vyřeš rovnici:
\(a-7(2a-7)=9-5a\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 7 / 20
7. Otázka
Vyřeš rovnici:
\(2(14-3x)-(4x+5)=x-6x+4(x-1)\)Správně
Špatně
Nejdříve odstraníme všechny závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 8 / 20
8. Otázka
Vyřeš rovnici:
\(3(x+8)-7(2-x)=10(x+1)\)Správně
Špatně
Nejdříve odstraníme všechny závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 9 / 20
9. Otázka
Vyřeš rovnici:
\(4+4(y-8)=6(3y-4)-5(8-5y)-3y\)Správně
Špatně
Nejdříve odstraníme všechny závorky.Pozor na znaménka. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 10 / 20
10. Otázka
Vyřeš rovnici:
\(11-3(7v+10)+(6v-13)=4v-3(2v+1)\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na znaménka. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 11 / 20
11. Otázka
Vyřeš rovnici:
\((8-3x)^2+(5-4x)^2-6=(9-5x)^2+20x-4\)Správně
Špatně
Nejdříve odstraníme závorky. Závorky jsou na druhou mocninu. Pro jejich výpočet využijeme algebraické vzorce \((a\pm b)^2=a^2\pm 2ab + b^2\).
Čísla potom dáme na jednu stranu, neznámou na druhou. Členy s druhou mocninou by se měli vyrušit.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek. -
Otázka 12 / 20
12. Otázka
Vyřeš rovnici:
\(2a+4(3-2a)+5(3a+1)=3(3a-7)-5\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 13 / 20
13. Otázka
Vyřeš rovnici:
\(4(5-2k)+3(2k-5)+4=3-2(k-3)\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou. Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 14 / 20
14. Otázka
Vyřeš rovnici:
\((x-1)^2-5=1-(x-1) \cdot (3-x)\)Správně
Nejdříve odstraníme závorky. Závorky jsou na druhou mocninu. Pro jejich výpočet využijeme algebraické vzorce \((a\pm b)^2=a^2\pm 2ab + b^2\). Závorky roznásobíme tak, že každý člen jedné závorky vynásobíme každým členem druhé zárovky, tj. každý s každým.
Čísla potom dáme na jednu stranu, neznámou na druhou. Členy s druhou mocninou by se měli vyrušit.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
Špatně
-
Otázka 15 / 20
15. Otázka
Vyřeš rovnici:
\(4(s+2)-7(2s-1)=30-9(3s-4)\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek. -
Otázka 16 / 20
16. Otázka
Vyřeš rovnici:
\((6a-5) \cdot (2a+1) =(4a-1) \cdot (3a-2)\)Správně
Špatně
Nejdříve odstraníme závorky. Závorky roznásobíme tak, že každý člen jedné závorky vynásobíme každým členem druhé zárovky, tj. každý s každým.
Čísla potom dáme na jednu stranu, neznámou na druhou. Členy s druhou mocninou by se měli vyrušit.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek. -
Otázka 17 / 20
17. Otázka
Vyřeš rovnici:
\((2u+7)^2-4=(u+4) \cdot (4u+15)\)Správně
Špatně
Nejdříve odstraníme závorky. Závorky jsou na druhou mocninu. Pro jejich výpočet využijeme algebraické vzorce \((a\pm b)^2=a^2\pm 2ab + b^2\). Závorky roznásobíme tak, že každý člen jedné závorky vynásobíme každým členem druhé zárovky, tj. každý s každým.
Čísla potom dáme na jednu stranu, neznámou na druhou. Členy s druhou mocninou by se měli vyrušit.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
-
Otázka 18 / 20
18. Otázka
Vyřeš rovnici:
\(5(a-3)-3(a-2)=2(a-12)-1\)Správně
Špatně
Nejdříve odstraníme závorky. Čísla potom dáme na jednu stranu, neznámou na druhou.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek. -
Otázka 19 / 20
19. Otázka
Vyřeš rovnici:
\((8y-1) \cdot (5+2y)=(4y+5)^2\)Správně
Špatně
Nejdříve odstraníme závorky. Závorky jsou na druhou mocninu. Pro jejich výpočet využijeme algebraické vzorce \((a\pm b)^2=a^2\pm 2ab + b^2\). Závorky roznásobíme tak, že každý člen jedné závorky vynásobíme každým členem druhé zárovky, tj. každý s každým.
Čísla potom dáme na jednu stranu, neznámou na druhou. Členy s druhou mocninou by se měli vyrušit.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek. -
Otázka 20 / 20
20. Otázka
Vyřeš rovnici:
\(7- \left[ 3-(8+3x) \right] =3(x+4)\)Správně
Špatně
Nejdříve odstraníme závorky. Závorky odstraňuje postupně, zevnitř ven. Nejdříve tedy odstraníme kulaté, potom teprve hranaté. Čísla potom dáme na jednu stranu, neznámou na druhou.
Při přechodu přes znaménko rovnosti, se členům dávají opačná znaménka. Členy na jednotlivých stranách spočítáme. Abychom dostali konečný výsledek, potřebujeme pouze jednu kladnou neznámou. Pokud je to potřeba, rovnici vydělíme a dostáváme konečný výsledek.
Lineární rovnice se zlomky
Procvičování lineárních rovnic se zlomky – 20 otázek
Lineární rovnice se zlomky
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičování lineárních rovnic se zlomky – 20 otázek
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Vyřeš rovnici:
\(\dfrac{a}{5}=-4\)Správně
Špatně
-
Otázka 2 / 20
2. Otázka
Vyřeš rovnici:
\(\dfrac{r}{2}-3=4\)Správně
Špatně
-
Otázka 3 / 20
3. Otázka
Vyřeš rovnici:
\(\dfrac{7}{3}-y=\dfrac{1}{3}\)Správně
Špatně
-
Otázka 4 / 20
4. Otázka
Vyřeš rovnici:
\(\dfrac{4}{3}+\dfrac{3}{5}+\dfrac{1}{2}=x\)Správně
Špatně
-
Otázka 5 / 20
5. Otázka
Vyřeš rovnici:
\(\dfrac{a}{3}+\dfrac{a}{6}=3\)Správně
Špatně
-
Otázka 6 / 20
6. Otázka
Vyřeš rovnici:
\(4-\dfrac{7-3x}{5}=3-\dfrac{3-7x}{10}+\dfrac{x+1}{2}\)Správně
Špatně
-
Otázka 7 / 20
7. Otázka
Vyřeš rovnici:
\(x-\dfrac{3x}{2}+5=\dfrac{2x}{3}+\dfrac{5x}{6}-\dfrac{5x}{6}-2\)Správně
Špatně
-
Otázka 8 / 20
8. Otázka
Vyřeš rovnici:
\(2(x+4)=\dfrac{2}{3}+x\)Správně
Špatně
-
Otázka 9 / 20
9. Otázka
Vyřeš rovnici:
\(\dfrac{3}{5}(2x-5)-\dfrac{x}{3}-\dfrac{1}{5}=\dfrac{4}{5}(3x-2)-\dfrac{2}{3}(5x-3)\)Správně
Špatně
-
Otázka 10 / 20
10. Otázka
Vyřeš rovnici:
\(\dfrac{5(x-3)}{6}-\dfrac{2x-12}{5}=\dfrac{3(x+4)}{15}-\dfrac{5-3x}{10}\)Správně
Špatně
-
Otázka 11 / 20
11. Otázka
Vyřeš rovnici:
\(\dfrac{2(x-4)}{3}+\dfrac{3x+1}{8}=\dfrac{5(x+2)}{12}-\dfrac{1-10x}{24}\)Správně
Špatně
-
Otázka 12 / 20
12. Otázka
Vyřeš rovnici:
\(\dfrac{y-4}{5}-\dfrac{7(3y-2)}{5}=\dfrac{9}{13}(9-2y)-(3y-5)\)Správně
Špatně
-
Otázka 13 / 20
13. Otázka
Vyřeš rovnici:
\(\dfrac{6x+1}{8}=0\)Správně
Špatně
-
Otázka 14 / 20
14. Otázka
Vyřeš rovnici:
\(x-3+\dfrac{x}{4}=\dfrac{x-5}{3}\)Správně
Špatně
-
Otázka 15 / 20
15. Otázka
Vyřeš rovnici:
\(\dfrac{x-1}{3}-2(1-4x)=\dfrac{x}{4}-\dfrac{7-52x}{6}\)Správně
Špatně
-
Otázka 16 / 20
16. Otázka
Vyřeš rovnici:
\(x(x^2-9)-(x-2)(x^2+2x+4)-\dfrac{5}{4}=0\)Správně
Špatně
-
Otázka 17 / 20
17. Otázka
Vyřeš rovnici:
\(6-\dfrac{3-2v}{5}\cdot2=4v\)Správně
Špatně
-
Otázka 18 / 20
18. Otázka
Vyřeš rovnici:
\(5-\dfrac{7-2x}{2}=-\dfrac{7}{6}-(11x-1):3\)Správně
Špatně
-
Otázka 19 / 20
19. Otázka
Vyřeš rovnici:
\(0,5s-\dfrac{3s-2}{6}+\dfrac{3s-1}{3}=2(s-1)\)Správně
Špatně
-
Otázka 20 / 20
20. Otázka
Vyřeš rovnici:
\(\dfrac{3}{4}(a-1)-\dfrac{a-1}{3}=\dfrac{1}{2}a-\dfrac{a}{3}+\dfrac{1}{12}\)Správně
Špatně
Malá násobilka
Procvičení malé násobilky – 20 otázek.
Malá násobilka
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičení malé násobilky – 20 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
\(4\cdot 4\)
Správně
Špatně
-
Otázka 2 / 20
2. Otázka
\(1\cdot 8\)
Správně
Špatně
-
Otázka 3 / 20
3. Otázka
\(9\cdot 8\)
Správně
Špatně
-
Otázka 4 / 20
4. Otázka
\(3 \cdot 5\)
Správně
Špatně
-
Otázka 5 / 20
5. Otázka
\(10\cdot 2\)
Správně
Špatně
-
Otázka 6 / 20
6. Otázka
\(3\cdot 3\)
Správně
Špatně
-
Otázka 7 / 20
7. Otázka
\(8\cdot 6\)
Správně
Špatně
-
Otázka 8 / 20
8. Otázka
\(4\cdot 7\)
Správně
Špatně
-
Otázka 9 / 20
9. Otázka
\(6\cdot 6\)
Správně
Špatně
-
Otázka 10 / 20
10. Otázka
\(2\cdot 8\)
Správně
Špatně
-
Otázka 11 / 20
11. Otázka
\(5\cdot 1\)
Správně
Špatně
-
Otázka 12 / 20
12. Otázka
\(7\cdot 10\)
Správně
Špatně
-
Otázka 13 / 20
13. Otázka
\(1\cdot 10\)
Správně
Špatně
-
Otázka 14 / 20
14. Otázka
\(1\cdot 7\)
Správně
Špatně
-
Otázka 15 / 20
15. Otázka
\(5\cdot 5\)
Správně
Špatně
-
Otázka 16 / 20
16. Otázka
\(10\cdot 9\)
Správně
Špatně
-
Otázka 17 / 20
17. Otázka
\(2\cdot 3\)
Správně
Špatně
-
Otázka 18 / 20
18. Otázka
\(6\cdot 2\)
Správně
Špatně
-
Otázka 19 / 20
19. Otázka
\(7\cdot 9\)
Správně
Špatně
-
Otázka 20 / 20
20. Otázka
\(9\cdot 4\)
Správně
Špatně
Soustava dvou lineárních dvojic
Procvičování lineárních soustav o dvou neznámých.
Soustava dvou lineárních dvojic
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičování lineárních soustav o dvou neznámých.
Výsledky jsou uvedeny pouze jako uspořádané dvojice. Nezapomínejte ale na to, že konečný výsledek je zapsán v oboru pravdivosti.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
\(\begin{eqnarray*}
-4x-3y&=&4\\
2x+5y&=&12\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 2 / 20
2. Otázka
\(\begin{eqnarray*}
4c+5d&=&-8\\
3c-4d&=&25\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 3 / 20
3. Otázka
\(\begin{eqnarray*}
r+s&=&5\\
4r+s&=&-4\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 4 / 20
4. Otázka
\(\begin{eqnarray*}
12y&=&11x-196\\
12x&=&13y+213\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 5 / 20
5. Otázka
\(\begin{eqnarray*}
2x-y-5&=&0\\
6x-3y-7&=&0\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 6 / 20
6. Otázka
\(\begin{eqnarray*}
x-3&=&-y\\
0,5x+y&=&4\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 7 / 20
7. Otázka
\(\begin{eqnarray*}
2(a+b)-3(a-b)&=&4\\
5(a+b)-7(a-b)&=&2\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 8 / 20
8. Otázka
\(\begin{eqnarray*}
4(x+2)&=&1-5y\\
3(y+2)&=&3-2x\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 9 / 20
9. Otázka
\(\begin{eqnarray*}
2,5x+0,2y&=&-4\\
0,2x+0,1y&=&\dfrac{1}{10}\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 10 / 20
10. Otázka
\(\begin{eqnarray*}
\dfrac{x}{3}+\dfrac{y}{2}&=&\dfrac{11}{12}\\
\dfrac{x}{2}+\dfrac{y}{3}&=&\dfrac{3}{4}\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 11 / 20
11. Otázka
\(\begin{eqnarray*}
x-2y&=&-5\\
\dfrac{x+y}{2}-\dfrac{2y-x}{5}&=&-1\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 12 / 20
12. Otázka
\(\begin{eqnarray*}
8-\dfrac{b}{3}&=&\dfrac{a-2b}{4}+\dfrac{a}{2}\\
\dfrac{2a+b}{5}-3&=&\dfrac{3a-5b}{2}\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 13 / 20
13. Otázka
\(\begin{eqnarray*}
(x+1)^2+(y+1)^2+10&=&x(x+6)+y(y+6)\\
(x+1)^2-(y-1)^2+8&=&x(x-6)-y(y-6)+8\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 14 / 20
14. Otázka
\(\begin{eqnarray*}
11-\dfrac{x+2}{5}&=&2y\\
\dfrac{x+1}{2}-\dfrac{y-2}{3}&=&1\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 15 / 20
15. Otázka
\(\begin{eqnarray*}
\dfrac{x}{3}&=&\dfrac{y+2}{6}-\dfrac{y-4}{2}\\
2x&=&2+\dfrac{4}{3}(y-1)\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 16 / 20
16. Otázka
\(\begin{eqnarray*}
\dfrac{x+2y}{5}&=&0,8\\
-\dfrac{1}{5}+3(-x+y)&=&-3-\dfrac{2}{10}\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 17 / 20
17. Otázka
\(\begin{eqnarray*}
4x-\frac{1}{7}y&=&\dfrac{1}{5}y-3x-\dfrac{1}{2}\\
(x+y)\cdot\dfrac{1}{6}&=&\dfrac{1}{5}(y-1)+x\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 18 / 20
18. Otázka
\(\begin{eqnarray*}
3(r+\dfrac{s}{2})-\dfrac{3r+s}{3}&=&-3\\
\dfrac{r+3}{5}-\frac{s+1}{2}&=&3,5\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 19 / 20
19. Otázka
\(\begin{eqnarray*}
\dfrac{1}{2}\left[2u+4(5-2v)\right]&=&\dfrac{1}{6}(-u+4)\\
u(u+2)-(u^2-9)&=&\dfrac{1}{7}\left[v-3(v-6)\right]\\
\end{eqnarray*}\)Správně
Špatně
-
Otázka 20 / 20
20. Otázka
\(\begin{eqnarray*}
\dfrac{\dfrac{12+6x}{24}}{1\dfrac{2}{12}}&=&8y-2(x+y)+4\\
3(x+y)-3y+25&=&\dfrac{\dfrac{4(x+1)}{5}}{\dfrac{1}{15}}\\
\end{eqnarray*}\)Správně
Špatně
Řešení pravoúhlého trojúhelníku
Procvičování výpočtů v pravoúhlém trojúhelníku pomocí goniometrických funkcí.
Řešení pravoúhlého trojúhelníku
Závěrečný přehled
Zodpovězeno 0 z 18 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
Information
Procvičování výpočtů v pravoúhlém trojúhelníku pomocí goniometrických funkcí.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 18 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 18
1. Otázka
Je dán pravoúhlý trojúhelník ABC.
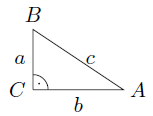
Stranu a spočítáme pomocí funkce \(\cos \gamma= \dfrac{b}{c}\)?
Správně
Špatně
Pravý úhel je u vrcholu C, což je úhel \(\gamma\). S pravým úhlem ve výpočtu nikdy nepočítáme.
-
Otázka 2 / 18
2. Otázka
Je dán trojúhelník XYZ. Strana y = 7, 16 cm a úhel \(\beta\) = 22° 23′.
Jak veliká je přepona daného trojúhelníku?Správně
Špatně
Chceme přeponu, tj. stranu z. Úhel \(\beta\) je u vrcholu Y. Na výpočet přepony využíváme funkci sinus nebo kosinus. Máme úhel a stranu k němu protilehlou, použijeme tedy \(\sin \beta = \dfrac{y}{z}\). Dosadíme, vyjádříme stranu z a spočítáme na kalkulačce.
-
Otázka 3 / 18
3. Otázka
Máme pravoúhlý trojúhelník ABC.
Strana a = 17, 4 cm, strana c = 18, 8 cm, úhel \(\alpha\) = 67° 37′.Jaká je velikost strany b a úhlu \(\beta\)?
Správně
Špatně
-
Otázka 4 / 18
4. Otázka
Vypočítejte délku přepony v trojúhelníku ABC s pravým úhlem při vrcholu C. Známe úhel \(\alpha\) = 15° a stranu b = 35 mm.
Správně
Špatně
-
Otázka 5 / 18
5. Otázka
Vypočtěte velikosti vnitřních úhlů pravoúhlého trojúhelníku, jestliže jeho odvěsny mají délky 185 mm a 32,4 cm.
Správně
Špatně
-
Otázka 6 / 18
6. Otázka
V pravoúhlém trojúhelníku XYZ máme délku přepony rovnu 8 cm a úhel \(\beta\) má 35°. Dopočítejte zbývající strany a úhel.
Správně
Špatně
-
Otázka 7 / 18
7. Otázka
Vypočítejte obsah pravoúhlého trojúhelníku ABC, u nějž známe:
a = 14,8 cm
\(\beta\) = 39° 20′.
Výsledek zaokrouhlete na celé číslo.Správně
Špatně
-
Otázka 8 / 18
8. Otázka
V pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C je dán úhel CAB = 60°. Strana AC má délku b = 6\(\sqrt{3}\).
Jaká je délka strany BC?
Jaká je velikost výsky na přeponu AB?Správně
Špatně
-
Otázka 9 / 18
9. Otázka
Rovnoramenný trojúhelník má výšku 10 cm a úhel u základny je 65°. Jaký je obvod trojúhelníku.
Správně
Špatně
-
Otázka 10 / 18
10. Otázka
Rovnoramenný trojúhelník má délku ramene 8 cm. Úhel u základny je 30°. Jaký je obvod a obsah trojúhelníku?
Správně
Špatně
-
Otázka 11 / 18
11. Otázka
Na břehu řeky jsou dva stromy vzdálené od sebe 50 m. Na protějším břehu stojí strom tak, že spolu s předchozími tvoří pravoúhlý trojúhelník, jehož druhou odvěsnou je šířka řeky. Urči šířku řeky, pokud přepona stromového trojúhelníku svírá s břehem úhel 67° .
Správně
Špatně
-
Otázka 12 / 18
12. Otázka
Na náměstí stojí proti sobě kostelní a radniční věž. Kostelní věž je vysoká 45 m a z jejího vrcholu je vidět pata radniční věže pod hloubkovým úhlem \(\alpha\) = 23° . Pata kostelní věže je z vrcholu radniční věže vidět pod hloubkovým úhlem \(\beta\) = 31°. Jaká je výška radniční věže. Jak dlouhé je náměstí?
Správně
Špatně
-
Otázka 13 / 18
13. Otázka
Na rovině se sázejí stromky ve vzdálenosti 3,5 metru. Jak daleko od sebe musíme kopat jamky pro řadu stromků v dané spádové přímce na svahu se sklonem 25°, chceme-li zachovat vodorovnou vzdálenost 3,5 metru.
Správně
Špatně
-
Otázka 14 / 18
14. Otázka
Z výšiny, ležící 80 m nad hladinou rybníka, je vidět mrak ve výškovém úhlu 56° a jeho odraz ve vodě v hloubkovém úhlu 58°. Jak vysoko je mrak nad hladinou rybníka? Výsledek zaokrouhlete na celé číslo.
Správně
Špatně
-
Otázka 15 / 18
15. Otázka
Pod jakým výškovým úhlem stoupá vozidlo do kopce, které ujelo 3 km a překonalo výškový rozdíl 250 metrů?
Správně
Špatně
-
Otázka 16 / 18
16. Otázka
Z pozorovatelny 20 metrů vysoké a vzdálené 15 metrů od břehu řeky je řeka široká 30 metrů. Pod jakým zorných úhlem vidí pozorovatel šířku řeky z vrcholu pozorovatelny?
Správně
Špatně
-
Otázka 17 / 18
17. Otázka
Jak dlouhý musí být žebřík k místu, které je 10 metrů vysoko nad zemí a svírá se stěnou úhel 32°. Výsledek zaokrouhlete na desetiny.
Správně
Špatně
-
Otázka 18 / 18
18. Otázka
Jak vysoká je budova, která na vodorovnou dlažbu vrhá stín dlouhý 69,2 m pod úhlem 37\(^{\circ}\)24′?
Správně
Špatně
Goniometrické funkce I
Procvičení výpočtů a vzorců s goniometrickými funkcemi – 20 otázek.
Goniometrické funkce I
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičení výpočtů a vzorců s goniometrickými funkcemi – 20 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Urči hodnotu goniometrických funkcí a vypočítej:
\(\dfrac{tg\: 60^{\circ}+tg \:30^{\circ}}{tg\: 60^{\circ}-tg\:30^{\circ}}\).Správně
Špatně
-
Otázka 2 / 20
2. Otázka
Zjednoduš výraz za předpokladu, že podmínky platí:
\(\dfrac{(sin\:x\cdot cotg\:x)^{2}-1}{3sin^{2}x}\)Správně
Špatně
-
Otázka 3 / 20
3. Otázka
Dokaž, že daný výraz platí:
\(\dfrac{1}{cos\:x}-sin\:x\cdot tg\:x = cos\:x\)Správně
Špatně
-
Otázka 4 / 20
4. Otázka
Dokaž, že daný výraz platí:
\(\dfrac{1-tg^{2}\dfrac{x}{2}}{1+tg^{2}\dfrac{x}{2}} = cos\:x\)Správně
Špatně
-
Otázka 5 / 20
5. Otázka
Pomocí vzorce pro poloviční argument urči hodnotu \(\sin 15^\circ\).
Správně
Špatně
-
Otázka 6 / 20
6. Otázka
Uprav výraz:
\(\dfrac{\sin2x}{\cos2x-\cos^{2}x}\)Správně
Špatně
-
Otázka 7 / 20
7. Otázka
Uprav výraz:
\(\dfrac{\cos^{4}x-\sin^{4}x}{\cos2x}\)Správně
Špatně
-
Otázka 8 / 20
8. Otázka
Uprav výraz za předpokladu, že má smysl:
\(\dfrac{2\sin^{2}x-\sin2x}{2\cos^{2}x-\sin2x}\)Správně
Špatně
-
Otázka 9 / 20
9. Otázka
Uprav výraz a urči podmínky:
\(\dfrac{\cos^{2}x-\cos2x}{\sin2x}\)Správně
Špatně
Nápověda
Správné odpovědi jsou POUZE dvě – jedna pro výsledek, druhá pro podmínku.
-
Otázka 10 / 20
10. Otázka
Zjednoduš výraz:
\(tg^{2}x\cdot \cos^{2}x+1-\cos^{2}x\)Správně
Špatně
-
Otázka 11 / 20
11. Otázka
Uprav výraz a urči podmínky:
\(\dfrac{5\sin^{2}x}{\cos\:x-1}\)Správně
Špatně
Nápověda
Správné odpovědi jsou POUZE dvě – jedna pro výsledek, druhá pro podmínku.
-
Otázka 12 / 20
12. Otázka
Uprav výraz:
\(\dfrac{\sqrt{1+cotg^{2}x}}{\sqrt{1+tg^{2}x}}\)Správně
Špatně
-
Otázka 13 / 20
13. Otázka
Uprav výraz:
\(\dfrac{1-\cos^{2}x}{1+tg^{2}x}-\dfrac{\cos^{2}x}{1+cotg^{2}x}+\dfrac{1}{\cos^{2}x}-1\)Správně
Špatně
-
Otázka 14 / 20
14. Otázka
Zjednoduš výraz:
\(\dfrac{\cos\:x}{1-\sin\:x}+\dfrac{\cos\:x}{1+\sin\:x}\)Správně
Špatně
-
Otázka 15 / 20
15. Otázka
Uprav výraz:
\(\left(\dfrac{1}{\sin\:x}+\sin\:x\right)^2+\left(\dfrac{1}{\cos\:x}+\cos\:x\right)^2\)Správně
Špatně
-
Otázka 16 / 20
16. Otázka
Uprav výraz:
\(\dfrac{\sin\:x}{tg\:x}+\dfrac{\cos\:x}{cotg\:x}\)Správně
Špatně
-
Otázka 17 / 20
17. Otázka
Uprav výraz:
\(4\sin^{2}x\cdot \cos^{2}x+\cos^{2}2x\)Správně
Špatně
-
Otázka 18 / 20
18. Otázka
Uprav výraz:
\(\dfrac{2\sin\:x+ \sin2x}{2\sin\:x- \sin2x}\)Správně
Špatně
-
Otázka 19 / 20
19. Otázka
Uprav výraz:
\(\cos^{2}2x+ \sin^{2}2x\)Správně
Špatně
-
Otázka 20 / 20
20. Otázka
Uprav výraz:
\(\dfrac{2\cos2x}{\sin2x-2\sin^{2}x}\)Správně
Špatně
Derivace I - jednoduché
Procvičování jednoduchých derivací – 20 otázek.
Derivace I - jednoduché
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičování jednoduchých derivací – 20 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Derivuj funkci:
\(y=((ln\:t)^{16})\)Správně
Špatně
-
Otázka 2 / 20
2. Otázka
Derivuj funkci:
\(y=cotg (2x+5)\)Správně
Špatně
-
Otázka 3 / 20
3. Otázka
Derivuj funkci:
\(y=12^{(6-2t)}\)Správně
Špatně
-
Otázka 4 / 20
4. Otázka
Derivuj funkci:
\(y=arctg (5x-2)\)Správně
Špatně
-
Otázka 5 / 20
5. Otázka
Derivuj funkci:
\(y=sin (x-3)\)Správně
Špatně
-
Otázka 6 / 20
6. Otázka
Derivuj funkci:
\(y=arccotg (3x+9)\)Správně
Špatně
-
Otázka 7 / 20
7. Otázka
Derivuj funkci:
\(y = 10^{(x-6)}\)Správně
Špatně
-
Otázka 8 / 20
8. Otázka
Derivuj funkci:
\(y = e^{(-6t)}\)Správně
Špatně
-
Otázka 9 / 20
9. Otázka
Derivuj funkci:
\(y = ln (1-t)\)Správně
Špatně
-
Otázka 10 / 20
10. Otázka
Derivuj funkci:
\(y = cotg(6x-3)\)Správně
Špatně
-
Otázka 11 / 20
11. Otázka
Derivuj funkci:
\(y = cos (7x)\)Správně
Špatně
-
Otázka 12 / 20
12. Otázka
Derivuj funkci:
\(y=19^{t}\cdot ln \:t\)Správně
Špatně
-
Otázka 13 / 20
13. Otázka
Derivuj funkci:
\(y=e^{x}\cdot \sin x\)Správně
Špatně
-
Otázka 14 / 20
14. Otázka
Derivuj funkci:
\(y=e^{x}\cdot cotg\: x\)Správně
Špatně
-
Otázka 15 / 20
15. Otázka
Derivuj funkci:
\(y=\dfrac{e^{x}}{ln\:x}\)Správně
Špatně
-
Otázka 16 / 20
16. Otázka
Derivuj funkci:
\(y = arccotg(-5t)\)Správně
Špatně
-
Otázka 17 / 20
17. Otázka
Derivuj funkci:
\(y = \sqrt {x}\cdot arctg \: x\)Správně
Špatně
-
Otázka 18 / 20
18. Otázka
Derivuj funkci:
\(y=(x^{2}-3x)cotg \:x\)Správně
Špatně
-
Otázka 19 / 20
19. Otázka
Derivuj funkci:
\(y=\dfrac{2^{x}}{\cos\:x}\)Správně
Špatně
-
Otázka 20 / 20
20. Otázka
Derivuj funkci:
\(y=e^{x}\cdot arcsin\:x-\dfrac{\sin\:x}{x}\)Správně
Špatně
Goniometrické funkce II
Procvičení goniometrických funkcí pomocí součtových vzorců a vzorců pro součet a rozdíl – 10 příkladů.
Goniometrické funkce II
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení goniometrických funkcí pomocí součtových vzorců a vzorců pro součet a rozdíl – 10 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Pomocí součtových vzorců vypočítej hodnotu funkce tangens daného úhlu:
\(tg\: 105^{\circ}\)Správně
Špatně
-
Otázka 2 / 10
2. Otázka
Pomocí součtový vzorců uprav výraz:
\(-\cos(\pi -x)\)Správně
Špatně
-
Otázka 3 / 10
3. Otázka
Uprav výraz:
\(\sqrt{8}\sin\left(\dfrac{\pi}{6}-x\right)\)Správně
Špatně
-
Otázka 4 / 10
4. Otázka
Uprav výraz:
\(\sin\left(x+\dfrac{\pi}{4}\right)+\sin\dfrac{3\pi}{2}\)Správně
Špatně
-
Otázka 5 / 10
5. Otázka
Uprav výraz:
\(\sin\left(x+90^{\circ}\right)-\cos\left(270^{\circ}+x\right)\)Správně
Špatně
-
Otázka 6 / 10
6. Otázka
Uprav výraz:
\(cotg\left(60^{\circ}+x\right)\)Správně
Špatně
-
Otázka 7 / 10
7. Otázka
Uprav na součin výrazů:
\(\cos\left(x-\dfrac{\pi}{4}\right) -\cos\left(\dfrac{\pi}{4}+x\right)\)Správně
Špatně
-
Otázka 8 / 10
8. Otázka
Uprav na součin výrazů:
\(\sin3y – \sin\left(y-\dfrac{\pi}{2}\right)\)Správně
Špatně
-
Otázka 9 / 10
9. Otázka
Uprav na součin výrazů:
\(\cos (60^{\circ}-\alpha) + \cos(\alpha-30^{\circ})\)Správně
Špatně
-
Otázka 10 / 10
10. Otázka
Uprav na součin výrazů:
\(\sin\left(x+\dfrac{\pi}{6}\right) + \sin\left(x+\dfrac{\pi}{6}\right)\)Správně
Špatně
Přijímačky
Vyzkoušíte si své znalosti a časové dovednosti.
Přijímačky
Závěrečný přehled
Zodpovězeno 0 z 14 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
Vyzkoušíte si své znalosti a časové dovednosti.
V našem zkušebním testu chybí rýsování – nezapomeňte si jej zopakovat.
Test obsahuje 14 otázek a můžete celkem získat 40 bodů.
Na test si udělejte čas 50 minut.
Nesmíte používat kalkulačku a tabulky. K dispozici můžete mít pouze papír, psací potřeby, své vědomosti a dobrou náladu.
Tak běžte do toho. Přejeme mnoho úspěchů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 14 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
-
Pokud Vám není nějaká odpověď jasná nebo si nevíte s některým příkladem rady, určitě nás kontaktujte.
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 14
1. Otázka
Bodové ohodnocení: 1Vypočtěte, o kolik větší je pětina čísla 13 než čtvrtina čísla 10.
(Výsledek uveďte v desetinném čísle)Správně
Špatně
pětina ze 13 – \(\dfrac{1}{5}\cdot 13\)
čtvrtina z 10 – \(\dfrac{1}{4}\cdot 10\)
o kolik = rozdíl
\(\dfrac{1}{5}\cdot 13-\dfrac{1}{4}\cdot 10=\dfrac{13}{5}-\dfrac{10}{4}\) -
Otázka 2 / 14
2. Otázka
Bodové ohodnocení: 3Vypočtěte:
2.1. \(100:\sqrt{4}+\sqrt{25}\cdot 3^2-3\cdot\sqrt{100-36}\)
2.2. \(\dfrac{\left(-\dfrac{2}{3}\right)^2\cdot\left(\dfrac{1}{7}\right)}{\left(\dfrac{3}{7}-1\dfrac{1}{2}\right):\dfrac{3}{8}}\)
Správně 3 / 3BodyŠpatně / 3 BodyMusíme dát pozor na to, jaké úpravy mají přednost – závorky, umocnění, odmocnění, násobení, dělení, sčítání, odčítání
2.1. \(100:2+5\cdot 9-3\cdot8\)
2.2. \(\dfrac{\dfrac{4}{9}\cdot\dfrac{1}{7}}{\left(\dfrac{3}{7}-\dfrac{3}{2}\right)\cdot\dfrac{8}{3}}=\dfrac{4}{63}\cdot\dfrac{1}{-\dfrac{15}{14}\cdot\dfrac{8}{3}}=\dfrac{4}{63}\cdot\dfrac{1}{\dfrac{-20}{7}}\) -
Otázka 3 / 14
3. Otázka
Bodové ohodnocení: 2Vypočtěte a výsledek zapište zlomkem v základním tvaru:
(Zlomkovou čárku zapište pomocí lomítka, např. jednu polovina = 1/2)
\(\dfrac{1}{4}:(0,7+\dfrac{5}{4})\)Správně
Špatně
\(\dfrac{1}{4}:(\dfrac{7}{10}+\dfrac{5}{4})=\dfrac{1}{4}:\dfrac{14+25}{20}=\dfrac{1}{4}\cdot\dfrac{20}{39}\)
-
Otázka 4 / 14
4. Otázka
Bodové ohodnocení: 4Zjednodušte:
(výsledný výraz nesmí obsahovat závorky)4.1. \((4a+2)^2-4a(2+3a)\)
4.2. \((4-3c)\cdot\dfrac{c}{2}-\dfrac{2+c}{4}\)
Správně 4 / 4BodyŠpatně / 4 Body4.1. \(16a^2+16a+4-8a-12a^2\)
4.2. \(\dfrac{c(4-3c)}{2}-\dfrac{2+c}{4}=\dfrac{2c(4-3c)-(2+c)}{4}\) -
Otázka 5 / 14
5. Otázka
Bodové ohodnocení: 4Řešte rovnici:
5.1. \(2(x+2)=4\)
5.2. \(2\cdot\dfrac{a+4}{3}-2a=\dfrac{4}{6}a+\dfrac{6}{9}\)
Přiřaďte
- 0
- 1
- NŘ
- -1
- -36
- -5
- 5
-
5.1.
-
5.2.
Správně 4 / 4BodyŠpatně / 4 Body5.1. \(2x+4=4⇒2x=4-4\)
5.2. \(2\cdot\dfrac{a+4}{3}-2a=\dfrac{4}{6}a+\dfrac{6}{9}\:/\cdot 18\\
6\cdot2(a+4)-36a=12a+12\) -
Otázka 6 / 14
6. Otázka
Bodové ohodnocení: 2Roman, Pavel a Zdenek šetřili na dovolenou. Roman ušetřil 6 000 Kč. Zdenek ušetřil jednu třetinu úspor Pavla a Romana. Všichni tři dohromady ušetřili čtyřikrát více než Pavel.
Neznámý počet korun, které uspořil Pavel, označte písmenem p a sestavte k úloze odpovídající rovnici s neznámou p.
(Pokud se v zápise vyskytne zlomek, použijte k jeho zápisu lomítko /.
Pro správnou odpověď prosím napište rovnici v pořadí Roman, Pavel, Zdenek.)Správně
Špatně
Roman …… 6 000,-
Pavel …….. p
Zdenek …..1/3(p+6000)
celkem …… 4p -
Otázka 7 / 14
7. Otázka
Bodové ohodnocení: 2Pavel, Roman a Zdenek šetřili na dovolenou. Roman ušetřil 6 000 Kč. Zdenek ušetřil jednu třetinu úspor Pavla a Romana. Všichni tři dohromady ušetřili čtyřikrát více než Pavel. (viz. předchozí úloha)
Neznámý počet korun, které uspořil Pavel, označte písmenem p a vypočítejte, kolik korun naspořil Pavel.
Správně
Špatně
6000 + p + 1/3(p + 6000)=4p/*3
18000+3p+p+6000=12p -
Otázka 8 / 14
8. Otázka
Bodové ohodnocení: 3Přiřaďte správné odpovědi:
a) \(65 \:min \cdot\: ………… = 3\: hod – 50\: min\)
b) \(0,5\: kg : 50\: g + 200\: mg \cdot 2\: g = …………… g\)
c) \(100 \:cm^3-2 \:l+0,5\: hl = …………… dm^3\)
Přiřaďte
- 2
- 10,4
- 48,1
- 104
- 0,0481
- 3
- 1
- 50
- 0,05
- 1,04
- 1 040
-
a)
-
b)
-
c)
Správně 3 / 3BodyŠpatně / 3 Bodya) \(3\: hod – 50\: min=3\cdot60-50=130:65\)
b) \(0,5\: kg : 50\: g + 200\: mg \cdot 2\: g =500:50+0,2\cdot 2\)
c) \(100 \:cm^3-2 \:l+0,5\: hl =0,1-2+50\)
-
Otázka 9 / 14
9. Otázka
Bodové ohodnocení: 3Je dán čtverec ABCD. Úhlopříčka čtverce je \(\sqrt{32}\).
A) Vypočtěte délku strany čtverce.
B) Vypočtěte obsah vybarvené části obrazce.
- A) Délka strany čtverce je (4) j. B) Obsah vybarvené části obrazce je (3,4, 3,44) j2.
Správně 3 / 3BodyŠpatně / 3 BodyA) Úhlopříčka rozdělí čtverec na 2 rovnoramenné pravoúhlé trojúhelníky. Pomocí Pythagorovi věty umíme spočítat délku strany čtverce.
\((\sqrt{32})^2=a^2+a^2\)B) Nevybarvené části obrazce vytvoří kruh s průměrem o délce strany. Vypočítáme obsah čtverce, od něj odečteme obsah kruhu a máme výsledek.
-
Otázka 10 / 14
10. Otázka
Bodové ohodnocení: 4Stará fotografie měla rozměry a = 10 cm a b = 6 cm. Při kopírování vznikla nová fotografie. Oba rozměry byly zvětšeny 2,5krát.
Rozhodněte, zda jsou následující tvrzení pravdivá nebo nepravdivá. Do odpovědi zapište Ano/Ne.
- Rozměry nové fotografie jsou v poměru 3:5 (Ne, ne, NE) Obvod nové fotografie je 80 cm (Ano, ano, ANO)
Správně 4 / 4BodyŠpatně / 4 BodyRozměry nové fotografie jsou 10*2,5 a 6*2,5.
Rozměry můžeme zkrátit na základní tvar a dostaneme potřebný poměr.
Obsah vypočítáme podle vzorce pro obsah obdélníku. -
Otázka 11 / 14
11. Otázka
Bodové ohodnocení: 2Jaký je objem krabičky, která nám vznikne slepením ze sítě na obrázku?
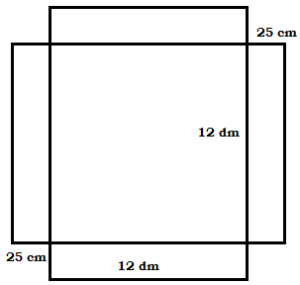Správně
Špatně
Objem tělasa spočítáme jako obsah podstavy vynásobený výškou. Pozor na jednotky.
-
Otázka 12 / 14
12. Otázka
Bodové ohodnocení: 2Vypočtěte velikost úhlu \(\beta\):
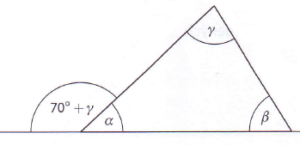Správně
Špatně
Víme, že úhel na celé přímce má velikost 180°. Místo úhlu alfa dosadíme (180°-(70°+ gama)). Trojúhelník nám dá v součtu 180°.
180° – 70° – gama + gama + beta = 180° -
Otázka 13 / 14
13. Otázka
Bodové ohodnocení: 2Hrnec je do 2/3 naplněn vodou. Dno má obsah 250 cm2. Do hrnce přilijeme 0,035 hl vody. O kolik cm stoupne hladina vody v hrnci?
Správně
Špatně
To, že je hrnec naplněn do 2/3 nás při výpočtu nezajímá. 0,035 hl je objem, který přiléváme a známe obsah podstavy. Dosadíme do vzorce pro výpočet objemu a získáme výšku.
-
Otázka 14 / 14
14. Otázka
Bodové ohodnocení: 6Vypočtěte a doplňte následující:
- Z 1 tuny cukrovky se vyrobí 200 kg cukru. K výrobě 0,6 tuny cukru, je potřeba 100 kg vody. Na 150 kg vody je potřeba (4500, 4 500) kg cukrovky. Zimní bunda stála 1 200 Kč. Byla zlevněna o 15 % a poté ještě jednou. Konečná cena bundy je 918 Kč. Při druhé slevě byla bunda zlevněna o (10) %. Cena sušenek byla před zdražením 15 Kč. Zdražení bylo ve výši 20 %. Po zdražení sušenky stojí (18) Kč.
Správně 6 / 6BodyŠpatně / 6 Body- Pomocí trojčlenky určíme, kolik cukrovky potřebujeme k výrobě 0,6 t cukru. Zjištěnou hodnotu dosadíme do druhé trojčlenky, pomocí níž získáme, kolik cukrovky je potřeba na 150 kg vody.
- Spočítáme cenu bundy po slevě. Tato cena bude v dalším výpočtu základ (100%) a dopočítáme procenta pro konečnou cenu.
- Pokud zdražujeme, můžeme spočítat dané procento a částku přičíst k původní, nebo můžeme rovnou spočítat cenu po zdražení (120%).
Vyjádření neznámé
Procvičení vyjadřování neznámé z různých typů vzorečků, rovnic – 15 otázek.
Vyjádření neznámé
Závěrečný přehled
Zodpovězeno 0 z 15 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Procvičení vyjadřování neznámé z různých typů vzorečků, rovnic – 15 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 15 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 15
1. Otázka
Vyjádři neznámou \(v_{a}\) ze vzorce:
\(S=\dfrac{1}{2}av_{a}\)Správně
Špatně
-
Otázka 2 / 15
2. Otázka
Vyjádři neznámou \(a\) ze vzorce:
\(S=2(ab+bc+ac)\)Správně
Špatně
-
Otázka 3 / 15
3. Otázka
Vyjádři neznámou \(\alpha\) ze vzorce:
\(l =l_{0}(1+ \alpha t)\)Správně
Špatně
-
Otázka 4 / 15
4. Otázka
Vyjádři neznámou \(t_{2}\) ze vzorce:
\(m_{1}c_{1}(t-t_{1}) = m_{2}c_{2}(t_{2}-t)\)Správně
Špatně
-
Otázka 5 / 15
5. Otázka
Vyjádři neznámou \(R\):
\(b = \dfrac{aR}{R+V}\)Správně
Špatně
-
Otázka 6 / 15
6. Otázka
Vyjádři neznámou \(R_{2}\) ze vzorce:
\(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}=\dfrac{1}{R}\)Správně
Špatně
-
Otázka 7 / 15
7. Otázka
Vyjádři neznámou \(\rho\) ze vzorce:
\(R =\rho \dfrac{l}{\pi \dfrac{d^{2}}{4}}\)Správně
Špatně
-
Otázka 8 / 15
8. Otázka
Ze vzorce vyjádři neznámou \(f\):
\(Z = -\dfrac{f}{a-f}\)Správně
Špatně
-
Otázka 9 / 15
9. Otázka
Vyjádři neznámou \(\rho_{2}\) ze vzorce:
\(V = \dfrac{\pi v}{6}(3\rho_{1}^{2}+3\rho_{2}^{2}+v^{2})\)Správně
Špatně
-
Otázka 10 / 15
10. Otázka
Vyjádři neznámou \(c\) ze vzorce:
\(u =\dfrac{u^{´}+v}{1+\dfrac{u^{´}v}{c^{2}}}\)Správně
Špatně
-
Otázka 11 / 15
11. Otázka
Vyjádři neznámou \(U_{1}\) ze vzorce:
\(N_{2}:N_{1}=U_{2}:U_{1}\)Správně
Špatně
-
Otázka 12 / 15
12. Otázka
Vyjádři neznámou \(v\) ze vzorce:
\(W =fmgs+ \dfrac{1}{2}mv^{2}\)Správně
Špatně
-
Otázka 13 / 15
13. Otázka
Vyjádři neznámou \(v\) ze vzorce:
\(S =2\pi r(r+v)\)Správně
Špatně
-
Otázka 14 / 15
14. Otázka
Vyjádři neznámou \(r_{1}\) ze vzorce:
\(Q =\sqrt{\dfrac{mgr_{1}^{3}}{2k\sqrt{l^{2}-\left(\dfrac{r_{2}}{2}\right)^{2}}}}\)Správně
Špatně
-
Otázka 15 / 15
15. Otázka
Vyjádři neznámou \(t\) ze vzorce:
\(E =\dfrac{m}{Q}\sqrt{\left(\dfrac{v}{t}\right)^{2}-g^{2}}\)Správně
Špatně
Převody jednotek
Procvičení převodů jednotek, které se mohou objevit u přijímacích zkoušek.
Převody jednotek
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení převodů jednotek, které se mohou objevit u přijímacích zkoušek.
Při výpočtech můžete využívat kalkulačky. Výsledky nevychází tak pěkně jako u přijímacích zkoušek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej:
A) 6 m + 1 250 cm = …………………. dm
B) 5 hod + 20 min – 3 600 s = ………………… minSprávně
Špatně
A) jednotky délky se mezi sebou posouvají o 10, z menší na větší ubíráme místa, naopak přidáváme.
Převedeme na požadované jednotky a sečteme.
B) jednotky času jsou po 60. Hodina má 60 min a minuta má 60 sekund.
Převedeme na požadované jednotky a sečteme/odečteme. -
Otázka 2 / 10
2. Otázka
Vypočítej:
A) 1 000 \(dm^2\) – 500 \(mm^2\) + 350 \(m^2\) = …………….. \(dm^2\)
B) 0,5 kg : 50 g + 200 mg \(\cdot \) 2 g = ……………. gSprávně
Špatně
A) jednotky obsahu se mezi sebou posouvají o 100, z menší na větší ubíráme místa, naopak přidáváme.
Převedeme na požadované jednotky a sečteme/odečteme.
B) přednost má násobení/dělení před sčítáním/odčítáním.
Abychom mohli násobit a dělit, musíme nejdříve převést na stejné jednotky. Jednotky hmotnosti nemají pevně stanovenou změnu mezi sebou. -
Otázka 3 / 10
3. Otázka
Doplň, aby platila rovnost:
A) 200 \(m^3\) + …………. \(l\) = 200,5 \(\cdot\) 1 000 \(dm^3\)
B) 5 \(t\) \(\cdot\) 0,5 \(kg\) = 500 \(kg\) + ……………. \(t\)Správně
Špatně
A) jednotky objemu se mezi sebou posouvají o 1 000, z menší na větší ubíráme místa, naopak přidáváme. Také víme, že litr je stejný jako decimetr krychlový.
Zjistíme hodnotu na pravé straně rovnice, od té odečteme známou hodnotu z levé strany rovnice a dostaneme výsledek. Pozor na jednotky!
B) zjistíme hodnotu na levé straně rovnice, od té odečteme známou hodnotu z pravé strany rovnice a dostaneme výsledek. Pozor na jednotky! -
Otázka 4 / 10
4. Otázka
Rozhodni, co je správně:
A) Testování trvá 3 hodiny a 20 minut. Můžeme říct, že je to stejná doba, jako 12 000 sekund.B) Objem krychle s hranou 5 metrů je stejný, jako objem nádrže, do které se vejde 12 500 litrů vody.
C) 3 sloni mají zásobu 4,2 tun krmiva na 7 dnů. Potom zásoba krmiva pro 6 slonů na 3 dny činí 3 500 kilo.
Správně
Špatně
A) převedeme na stejné jednotky a zjistíme, jestli je to správně
B) spočítáme objem krychle, převedeme na potřebné jednotky a zjistíme, jestli jsou objemy stejné
C) spočítáme, kolik krmiva potřebuje jeden slon na jeden den. Potom vynásobíme počtem slonů a dní a zjistíme, celkovou spotřebu. -
Otázka 5 / 10
5. Otázka
Zjisti:
A) Kolik minut je pět tisícin ze tří minut a 120 sekund?B) Kolik litrů jsou tři setiny z 20 \(m^3\)?
Správně
Špatně
A) nejdříve převedeme všechno na stejné jednotky – minuty, poté spočítáme pět tisícin, tj. 0,005, anebo ve zlomku, krát výsledek v minutách
B) převedeme metry krychlové na litry a vynásobíme 0,03 anebo zlomkem -
Otázka 6 / 10
6. Otázka
Cyklista jede rychlostí 15 km/h. Kolik kilometrů ujede za 20 minut?
Správně
Špatně
Spočítáme, za kolik minut ujede 15 km. Dotazované minuty podělíme minutami ze zadání a vynásobíme počtem kilometrů.
Jiná možnost výpočtu by byla spočítat, kolik km ujede za minutu a poté vynásobit poptávaným počtem minut.
-
Otázka 7 / 10
7. Otázka
Jana s Honzou si dali závody v běhu. Jana uběhne za 120 minut 14 kilometrů. Jakou minimální rychlostí (v m/s) musí běžet Honza, aby Janu předběhl?
Výsledek zaokrouhli na 2 desetinná místa.Správně
Špatně
Výsledek má být v m/s, převedeme si tedy čas Jany na sekundy a uběhnutou vzdálenost na metry. Jak nám napovídají jednotky, podělíme dráhu časem a dostaneme její požadovanou rychlost.
Aby Honza Janu předběhl, musí běžet rychleji. -
Otázka 8 / 10
8. Otázka
Na 3 porce zapečených brambor potřebujeme:
– půl kila brambor
– 1/4 kila masa
– 750 ml mléka
– sůl
– kořeníKolik gramů brambor, kilo masa a litrů mléka budeme potřebovat na 5 porcí?
Zaokrouhlujeme až konečné výsledky podle normy!Správně
Špatně
Všechny suroviny podělíme počtem porcí, pro kterou jsou stanoveny a vynásobíme požadovaným počtem porcí.
Jednotky můžeme upravit ještě před výpočty anebo nejdříve spočítáme a poté teprve zapíšeme ve správných jednotkách. -
Otázka 9 / 10
9. Otázka
Vypočítej:
A) \(\dfrac {10}{100}\) ze 100 l + \(\dfrac {2}{100}\) z 200 \(dm^3\) – \(\dfrac {4}{5}\) z 1 \(m^3\) = ……………… l
– výsledek uveď v desetinném čísleB) tři setiny z půl kila + pět šestin z 180 dekagramů = ………………… g
Správně
Špatně
Vypočítáme jednotlivé podíly, převedeme na stejné jednotky a dopočítáme.
-
Otázka 10 / 10
10. Otázka
Délka kroku syna je 50 cm. Délka kroku jeho otce je 0,7 m. Na společném výletě ušel otec 300 kroků. Ušel více kroků otec nebo syn? O kolik?
Správně
Špatně
Víme, kolik kroků ušel otec. Počet vynásobíme délkou kroku a zjistíme, jakou dráhu ušli. Dráhu podělíme délkou kroku syna a dostaneme se k výsledku.
Pozor na jednotky.
Přímá/nepřímá úměra, procenta
Procvičení přímé a nepřímé úměry a příkladů s procenty.
Přímá/nepřímá úměra, procenta
Závěrečný přehled
Zodpovězeno 0 z 15 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Procvičení přímé a nepřímé úměry, důležité je správně se ptát – čím míň tím víc/čím míň tím míň, …..
Procvičení příkladů s procenty. Dávejte pozor to tvoří základ. Od toho se sestavení trojčlenky odvíjí.
Celkem 15 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 15 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 15
1. Otázka
Osm švadlen by danou zakázku zhotovilo za 15 směn. Kolik švadlen musí na zakázce pracovat, aby byla zhotovena o 3 směny dříve?
Správně
Špatně
Jedná se o nepřímou úměru – čím míň odpracovaných směn, tím více švadlen musí pracovat.
Sestavíme trojčlenku, naznačíme směry a podle šipek sestavíme rovnici. -
Otázka 2 / 15
2. Otázka
Ze 3 tun cukrovky se vyrobí 480 kg cukru. Kolik tun cukru se vyrobí ze 17,5 tuny cukrovky?
Správně
Špatně
Jedná se o přímou úměru – čím víc cukrovky, tím více vyrobeného cukru.
Sestavíme trojčlenku, naznačíme směry a podle šipek sestavíme rovnici.
Pozor na jednotky, musí být v trojčlence stejné! -
Otázka 3 / 15
3. Otázka
3 stejně výkonné kombajny sklidí obilí za 12 dnů. Kolik kombajnů je třeba, aby obilí bylo sklizeno za 9 dní?
Správně
Špatně
Jedná se o nepřímou úměru – čím míň dnů, tím více kombajnů musí pracovat.
Sestavíme trojčlenku, naznačíme směry a podle šipek sestavíme rovnici. -
Otázka 4 / 15
4. Otázka
Osm zedníků za směnu spotřebuje 880 cihel. Kolik zedníků bylo na stavbě, jestliže skladník vydal celkem 1320 cihel?
Správně
Špatně
Jedná se o přímou úměru – čím více zedníků, tím více spotřebovaných cihel.
Sestavíme trojčlenku, naznačíme směry a podle šipek sestavíme rovnici. -
Otázka 5 / 15
5. Otázka
Nakupující po 8 % slevě zaplatil za zboží 2 737 Kč. Kolik stálo zboží před slevou?
Správně
Špatně
Procenta jsou vždy přímá úměra. Sestavíme trojčlenku, základ je vždy 100%.
Známe cenu po 8% slevě, můžeme počítat dvěma způsoby:
– 100% – 8% = 92%, to odpovídá ceně po slevě. Spočítáme 8%, přičteme k ceně a dostaneme původní cenu zboží.
– 100% neznámá, 92% je cena po slevě. Sestavíme trojčlenku, spočítáme a dostaneme cenu před slevou. -
Otázka 6 / 15
6. Otázka
Na skladě je 250 tun uhlí. První den odvezli 12%, druhý den 20% zbytku. Kolik tun uhlí pak zbyde na skladě?
Správně
Špatně
Procenta jsou vždy přímá úměra. Sestavíme trojčlenku, základ je vždy 100%.
Procenta NELZE sčítat.
Spočítáme, kolik tun uhlí odvezli první den. Druhý den odvezli 20% zbytku, tj. od původního množství odečteme tuny, které odvezli první den a teprve z tohoto výsledku spočítáme požadovaných 20%.
Celý příklad také můžete počítat druhou metodou, kde rovnou spočítáme, kolik zbyde první den na skladě, tj. 88% a toto množství bude základem pro výpočet druhého dne, kde opět můžeme počítat rovnou 80% a dostaneme hned výsledek. -
Otázka 7 / 15
7. Otázka
Bratr dostal minulý měsíc plat 15 000 Kč. Také dostal prémii ve výši 25 % jeho měsíční mzdy. Kolik peněz dostal celkem?
Správně
Špatně
Procenta jsou vždy přímá úměra. Sestavíme trojčlenku, základ je vždy 100%.
Ze zadání známe základ, spočítáme tedy 15%. Výsledek přičteme k základu a zjistíme, jaký celkový plat dostal.
Druhá varianta výpočtu by byla, že spočítáme 115% a tím dostaneme rovnou celkovou mzdu. -
Otázka 8 / 15
8. Otázka
Zahradnictví má připravit 6 000 ks sazenic rajčat pro drobný prodej. Klíčivost semen je 80 %, množství uhynulých rostlin z vyklíčených je 15 %. Kolik semen musejí v zahradnictví připravit, aby mohli zajistit dodávku 6 000 ks sazenic?
Správně
Špatně
Procenta jsou vždy přímá úměra, základ je 100%.
Musíme počítat popstupně, procenta NELZE sčítat.
6 000 sazenic musí zůstat již po procentu uhynutí. Tzn., že 6 000 je pouze 85% a spočítáme tedy 100%. Výsledek bude opět část sazenic, která zůstane po klíčivosti, tj. pouze 80%. Spočítáme opět 100% a dostaneme potřebný počet semen k vysazení. -
Otázka 9 / 15
9. Otázka
Do jazykového kurzu přibyl 1 nový student. Počet studentů se tím zvýšil o 6 %. Kolik studentů nyní navštěvuje jazykový kurz?
Správně
Procenta jsou vždy přímá úměra, základ je 100%.
1 student tvoří 6%. Spočítáme tedy 100% a nesmíme zapomenout přičíst nového studenta. Také můžeme rovnou spočítat 106% a dostaneme konečný počet studentů.Špatně
-
Otázka 10 / 15
10. Otázka
Jana nasbírala za hodinu 1 kg borůvek. Petra o čtvrtinu méně než Jana.
Petra sbírala celkem 3 hodiny, což je o třetinu méně, než sbírala Jana.
\(\begin{array}{|l|c|c|}
\hline \text{} & \text{Jana} & \text {Petra} \\\hline
\text{Nasbíráno za hodinu} & \text{}& \text {} \\\hline
\text{Počet odsbíraných hodin} & \text{}& \text {} \\\hline
\text{Nasbíráno celkem} & \text{}& \text {} \\\hline
\end{array}\)
A) O kolik procent více hodin odsbírala Jana než Petra?
B) O kolik procent méně borůvek nasbírala celkem Petra než Jana?Počítejte na 4 desetinná místa.
Správně
Špatně
Procenta jsou vždy přímá úměra, základ je 100%.
Nejdříve musíme doplnit tabulku, abychom potom měli z čeho počítat procenta. Pro výpočet je důležité přiřadit správně základ.
A) Základem je Petra
B) Základem je Jana -
Otázka 11 / 15
11. Otázka
Honza přišel na koncert o 15 minut později a tím promeškal osminu koncertu. Tomáš přišel půl hodiny po začátku koncertu. Kolik procent koncertu zmeškal Tomáš?
Správně
Špatně
-
Otázka 12 / 15
12. Otázka
Měsíc před prázdninami byla místa v kempu zamluvena z 20 %. Týden před prázdninami byl kemp obsazen ze tří čtvrtin a k zarezervování zbylo ještě 50 míst. Kolik míst bylo zamluveno měsíc před prázdninami?
Správně
Špatně
-
Otázka 13 / 15
13. Otázka
Střední školu navštěvuje 55 % chlapců. 15 % chlapců se učí německý jazyk a anglický jazyk se učí zbývajících 204 chlapců. Kolik děvčat chodí na střední školu?
Správně
Špatně
-
Otázka 14 / 15
14. Otázka
Na obdélníkovém pozemku s rozměry 35 m a 18,5 m je postaven dům se čtvercovým půdorysem o straně 14 m. Kolik procent pozemku není zastavěno?
Správně
Špatně
-
Otázka 15 / 15
15. Otázka
Do odborného učiliště chodí 850 žáků. V pololetí mělo 221 žáků vyznamenání a 18 % žáků mělo jednu nedostatečnou.
A) Kolik žáků mělo jednu nedostatečnou?
B) Kolik procent žáků nemělo vyznamenání ani nedostatečnou?Správně
Špatně
Poměr, měřítko mapy
Procvičení poměru a měřítka mapy. Dávejte pozor, v jakých jednotkách máte měřítko – 10 otázek
Poměr, měřítko mapy
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení poměru a měřítka mapy. Dávejte pozor, v jakých jednotkách máte měřítko – 10 otázek
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Uprav poměr 200 : 350.
a) rozšiř \(\dfrac{1}{10}\),b) zkrať 5,
c) zapiš v základním tvaru.
Správně
Špatně
a) oba členy poměru vynásobíme 1/10
b) oba členy poměru vydělíme 5
c) oba členy poměru dělíme vždy stejným číslem tak dlouho, dokud už jednotlivé členy dělit nejdou a máme celé číslo
-
Otázka 2 / 10
2. Otázka
Fotografie s rozměry 12 cm a 15 cm se má
a) upravit v poměru 5:3,
b) upravit v poměru 1:3.
Jak velká bude fotografie? Došlo ke zvětšení nebo zmenšení?
Správně
Špatně
a) poměr je větší než 1, jedná se o zvětšení
jednotlivé rozměry vynásobíme prvním členem poměru a výsledek vydělíme druhým členem poměru
b) poměr je menší než 1, jedná o zmenšení
jednotlivé rozměry vynásobíme prvním členem poměru a výsledek vydělíme druhým členem poměru
Nápověda
Správně je jedna odpověď na každou otázku.
-
Otázka 3 / 10
3. Otázka
V podniku na výrobu počítačů je zaměstnáno celkem 1 188 pracovníků. Vývojových pracovníků je 540 a zbytek tvoří výrobní pracovníci. V jakém poměru jsou počty vývojových a výrobních pracovníků?
Správně
Špatně
Nejdříve spočítáme, kolik je výrobních pracovníků. Od celkové počtu odečteme vývojové pracovníky.
Počet jednotlivých pracovníků dáme do poměru – POZOR, musíme zachovat pořadí z otázky. Poměr upravíme na základní tvar. -
Otázka 4 / 10
4. Otázka
Budeme připravovat třičtvrtě litru perlivého nápoje z jablečného džusu, toniku a vody. Poměr jednotlivých nápojů je 5 : 3 : 7. Kolik ml vody, džusu a toniku budeme potřebovat?
Správně
Špatně
Třičtvrtě litru = 750 ml.
K jednotlivým surovinám známe poměrnou část. Abychom správně naředili, musíme celkový objem vydělit součtem poměrů. Dostaneme hodnotu jednoho dílku poměru a tím vynásobíme jednotlivé poměry. Získáme množství, které odpovídá dané surovině.
Pozor na uspořádání! -
Otázka 5 / 10
5. Otázka
Strany lichoběžníku jsou v poměru 2 : 5 : 7 : 3. Nejkratší strana měří 1,4 dm. Vypočítej v\(\nobreakspace\)cm obvod lichoběžníku.
Správně
Špatně
Potřebujeme zjistit hodnotu jednoho poměrného dílku. Známe délku nejkratší strany a tu přiřadíme k nejmenšímu číslu z poměru. Vydělíme délku poměrem a získáme hodnotu jednoho dílku. Touto hodnotou přenásobíme zbývající čísla v poměru a dostaneme výsledky jednotlivých stran.
Obvod lichoběžníku spočítáme tak, že sečteme všechny strany lichoběžníku. -
Otázka 6 / 10
6. Otázka
Tomáš s Lukášem vsadili Sportku. Jejich vložené peníze jsou v poměru 7 : 8. Dohodli se, že v daném poměru rozdělí i případnou výhru. Vyhráli 3 000 Kč. Lukáš vložil 160 Kč. Kolik korun vložil Tomáš a kolik vyhrál Lukáš?
Správně
Špatně
Zjistíme, které číslo z poměru odpovídá vložené částce Lukáše. Podělíme částku odpovídajícím poměrem, dostaneme hodnotu jednoho dílku poměru a vynásobíme poměrové číslo Tomáše – zjistíme, kolik vložil Tomáš.
Výherní částku vydělíme součtem poměrů. Dostaneme hodnotu jednoho dílu poměru a vynásobíme jednotlivé poměry. Tím zjistíme, kolik korun který chlapec vyhrál. -
Otázka 7 / 10
7. Otázka
Na mapě v měřítku 1:400 000 je vzdušná vzdálenost Hradce Králové od Jičína 10,5 cm. Jaká je skutečná vzdálenost těchto měst?
Správně
Špatně
Zkontrolujeme jednotky. Měřítko, pokud není uvedeno jinak, je vždy v centimetrech.
Měřítko vydělíme vzdáleností na mapě a dostaneme vzdálenost ve skutečnosti. Většinou skutečnou vzdálenostu uvádíme v metrech nebo v kilometrech. -
Otázka 8 / 10
8. Otázka
Urči měřítko mapy, na které je vzdálenost 1,04 km znázorněna úsečkou v délce 52 mm.
Správně
Špatně
Abychom dostali měřítko mapy, dáme zadané vzdálenosti do poměru. Pozor na jednotky!
Víme, že měřítko mapy se udává v centimetrech. -
Otázka 9 / 10
9. Otázka
Cyklista ujede 3,6 km za 12 min. Trasa, kterou ujede za půl hodiny, měří na mapě 1,8 dm. Rychlost cyklisty se nemění. Jaké je měřítko mapy?
Správně
Špatně
Nejdříve musíme spočítat, jakou vzdálenost ujede za 30 minut. Můžeme využít pro výpočet trojčlenku anebo zjistíme, kolik km ujede za minutu a vynásobíme to 30 minutami.
Potom už jen dáme do poměru ujetou vzdálenost a vzdálenost na mapě. Pozor na jednotky. -
Otázka 10 / 10
10. Otázka
Pan Nový cestuje z Říčan do Poděbrad. Vzdálenost měst na mapě je 86 mm. Průměrná rychlost auta je 80 km/hod. Cestoval 32,25 min. Jaká je vzdálenost obou měst a v jakém měřítku je mapa?
Správně
Špatně
Když víme, jak dlouho jel a jakou rychlostí, můžeme spočítat vzdálenost měst ve skutečnosti. Na výpočet můžeme využít trojčlenku, nebo zjistíme, kolik km ujede za minutu a vynásobíme počtem ujetých minut.
Dáme do poměru vzdálenost měst na mapě i ve skutečnosti a zjistíme měřítko mapy. Pozor na jednotky.
Rovnice - přijímačky
Procvičení lineárních rovnic obecných a se zlomky – 10 příkladů.
Rovnice - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení lineárních rovnic obecných a se zlomky – 10 příkladů.
Nezapomenťe provádět zkoušky, i když to není v požadavcích. Zkouška je Vaše výhoda, protože si ověříte svůj výpočet.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vyřeš rovnici:
\( \dfrac{x+6}{4}=x\)Správně
Špatně
V rovnici máme zlomek, musíme ho tedy odstranit. Celou rovnici vynásobíme společným násobkem jmenovatelů. Nesmíme zapomenout, že násobíme každý člen celé rovnice. Upravíme, převedeme neznámou na jednu stranu a čísla na druhou. Pokud nemáme ihned jednu kladnou neznámou, podělíme rovnici a dostaneme výsledek.
-
Otázka 2 / 10
2. Otázka
Vyřeš rovnici:
\( 3[3(3x-3)]-6(6-6x)=9(9-9x)\)Správně
Špatně
V rovnici máme závorky. Upravíme nejdříve levou i pravou stranu rovnice podle toho, co má přednost – odstraníme závorky od vnitřních po vnější. Upravíme, převedeme neznámou na jednu stranu a čísla na druhou. Pokud nemáme ihned jednu kladnou neznámou, podělíme rovnici a dostaneme výsledek.
-
Otázka 3 / 10
3. Otázka
Vyřeš rovnici:
\( 6(x+0,15)=3(3x+0,75)\)Správně
Špatně
-
Otázka 4 / 10
4. Otázka
Vyřeš rovnici:
\( 3(b-3)+4=b+2(b-1)\)Správně
Špatně
-
Otázka 5 / 10
5. Otázka
Vyřeš rovnici:
\( 3\cdot x=2,1x\)Správně
Špatně
-
Otázka 6 / 10
6. Otázka
Vyřeš rovnici:
\( 6c-2(2c-3)=3(c+1)-(4c-5)\)Správně
Špatně
-
Otázka 7 / 10
7. Otázka
Vyřeš rovnici:
\( \dfrac{5}{6}(a+2)-\dfrac{5}{6}=-\dfrac{1}{4}(3a-1)-1\)Správně
Špatně
-
Otázka 8 / 10
8. Otázka
Vyřeš rovnici:
\( 4\dfrac{x-4}{9}-\dfrac{3x+5}{6}=\dfrac{1}{2}\)Správně
Špatně
-
Otázka 9 / 10
9. Otázka
Vyřeš rovnici:
\( \dfrac{y}{2}\cdot \dfrac{3}{2}-\dfrac{1}{6}y=\dfrac{2}{3}-\dfrac{y}{2}\)Správně
Špatně
-
Otázka 10 / 10
10. Otázka
Vyřeš rovnici:
\( \dfrac{2}{3}\left[y-2y\left(\dfrac{8}{6}-\dfrac{1}{2}\right)\right]=y-\dfrac{3}{8}\)Správně
Špatně
Rovnice - slovní - přijímačky
Procvičení čtyř typů slovních úloh vedoucí na lineární rovnici – 15 otázek
Rovnice - slovní - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 15 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Procvičení čtyř typů slovních úloh vedoucí na lineární rovnici – 15 otázek
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 15 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 15
1. Otázka
Aritmetický průměr tří čísel je 12. První číslo je trojnásobkem čísla 5, druhé číslo je druhá mocnina čísla 4. Urči třetí číslo.
Správně
Špatně
-
Otázka 2 / 15
2. Otázka
5 litrů bílého vína a 9 litrů sudového červeného vína stojí celkem 946 Kč. 1 litr bílého vína je přitom o 4 Kč levnější než 1 litr červeného. Kolik stojí 7 litrů bílého vína a 8 litrů červeného?
Správně
Špatně
-
Otázka 3 / 15
3. Otázka
Brigádníci sklízeli 3 dny vinnou révu, celkem jí bylo 251 hlav. Druhý den sklidili o 48 hlav méně než první den, třetí den o 25 % více než první den. Kolik hlav révy sklidili brigádníci druhý a třetí den?
Správně
Špatně
-
Otázka 4 / 15
4. Otázka
Dvě auta proti sobě ve stejný okamžik vyjela rychlostí 100 km/h a 80 m/h. Místa startu byla od sebe vzdálena 240 km. Za jak dlouho se automobily setkaly?
Správně
Špatně
-
Otázka 5 / 15
5. Otázka
Z kasáren vyjela kolona vojenských aut rychlostí 35 km/h. Za 1 h 30 min byla za kolonou vyslána motospojka jedoucí průměrnou rychlostí 85 km/h. Za jak dlouho a v jaké vzdálenosti od kasáren dohoní motospojka kolonu?
Správně
Špatně
-
Otázka 6 / 15
6. Otázka
V 8 hodin vyšel Pepa z Hůrky do Lhotky rychlostí 3 km/h a v 9 hodin vyšel Tonda ze Lhotky do Hůrky rychlostí 5 km/h. Jak daleko od sebe jsou obě vesnice, jestliže se Pepa s Tondou potkali v 9.30hodin?
Správně
Špatně
-
Otázka 7 / 15
7. Otázka
Roznést letáky trvá Daliborovi 9 h, stejná práce by Kamile trvala 18 h. Jak dlouho by jim práce trvala, pokud by letáky roznášeli společně?
Správně
Špatně
-
Otázka 8 / 15
8. Otázka
Bazén se naplní za 18 min a vyprázdní se za 20 min. Za kolik hodin se bazén naplní, jestliže se bude naráz plnit a vypouštět?
Správně
Špatně
-
Otázka 9 / 15
9. Otázka
Tomáš a Pavel společně postavili zeď za 8 hodin. Tomáš sám ji postaví za 12 hodin. Jak dlouho by stavěl sám Pavel?
Správně
Špatně
-
Otázka 10 / 15
10. Otázka
Kolikaprocentní ocet získáme smícháním tří litrů devítiprocentního octa se dvěmi litry pětiprocentního octa?
Správně
Špatně
-
Otázka 11 / 15
11. Otázka
Chceme připravit 250 g 64%ního lihu. Máme 70%ní líh, který budeme ředit vodou. Kolik 70%ního lihu a kolik vody budeme potřebovat?
– výsledek zaokrouhli na celé g podle normySprávně
Špatně
Nápověda
Voda je 0%tní lihovina.
-
Otázka 12 / 15
12. Otázka
Kolikaprocentní roztok získáme, smícháme-li 250 g 32%ního roztoku NaCl a 0,4 kg 45%ního roztoku NaCl?
Správně
Špatně
-
Otázka 13 / 15
13. Otázka
Pro nakládání zeleniny je potřeba připravit 5 l roztoku soli o koncentraci 13,5%. Máme k dispozici 17% a 12% roztoky kuchyňské soli (NaCl). Kolik kterého roztoku je potřeba smíchat?
Správně
Špatně
-
Otázka 14 / 15
14. Otázka
V 7 hodin vyjelo z města X nákladní auto rychlostí 40 km/hod. Proti němu z města Y vyjelo osobní auto rychlostí 70 km/hod. Osobní automobil vyjel v 8 hod 30 min. Vzdálenost měst je 225 km. V kolik hodin a jak daleko od města Y se potkají?
Správně
Špatně
-
Otázka 15 / 15
15. Otázka
Do knihovny bylo během roku zakoupeno 120 nových knih. Za 2. pololetí jich přitom přibylo do knihovny o 40% více než za 1. pololetí. Kolik knih bylo do knihovny zakoupeno v 2. pololetí?
Správně
Špatně
Obvody a obsahy obrazců - přijímačky
Procvičení výpočtů Pythagorovi věty, obvodů a obsahů pro různé obrazce – 10 příkladů.
Obvody a obsahy obrazců - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení výpočtů Pythagorovi věty, obvodů a obsahů pro různé obrazce – 10 příkladů.
Můžete používat kalkulačku, příklady nevychází tak pěkně jako u přijímacích testů.
Za proměnnou \(\pi\) vždy dosazujte hodnotu 3,14.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Obsah velkého čtverce je \(100\: cm^{2}\). Vypočítej obsah nevybarvené části obrazce.
Správně
Špatně
Z obsahu umíme vypočítat délku strany velkého čtverce. Tato délka nám také tvoří průměr kruhu vepsaného do čtverce a zároveň je to úhlopříčka malého čtverce.
Úhlopříčka nám vytvoří pravoúhlý trojúhelník, použijeme Pythagorovu větu a protože jsou obě strany trojúhelníku stejně dlouhé, umíme vypočítat délku strany malého čtverce.
Vypočítáme obsah malého čtverce a ten odečteme od obsahu velkého. Rozdíl obsahů vytvoří zbývající prostor. -
Otázka 2 / 10
2. Otázka
Strom je vysoký 15 metrů. Koruna tvoří 2/3 výšky. Obsah kmene je \(20\: m^{2}\) a větve jej přesahují na každé straně o 2,5 metru. Jaký je obsah koruny vyobrazeného stromu?
Správně
Špatně
Vypočítáme 2/3 z celkové výšky – dostaneme výšku koruny v metrech. Výšku koruny odečteme od výšky stromu a dostaneme výšku kmene, tj. jedna strana obdélníku. Známe obsah kmene, umíme tedy dopočítat délku druhé strany obdélníku. Větve přesahují kmen z každé strany – délky sečteme a přičteme šířku kmene. Vypočítáme obsah jednoho trojúhelníku a vynásobíme dvěma, abychom dostali obsah celé koruny.
-
Otázka 3 / 10
3. Otázka
Obsah nejmenšího ze čtverců je \(25\:cm^{2} \). Urči v decimetrech součet obvodů všech čtverců. Výsledek zaokrouhli na 1 desetinné místo.
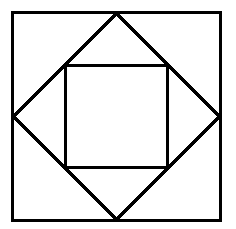Správně
Špatně
Z obsahu čtverce umíme vypočítat délku strany. Když se podíváte na obrázek pozorně, úhlopříčka menšího čtverce je zároveň délkou strany většího čtverce. Pomocí Pythagorovi věty tedy dopočítáme úhlopříčky jednotlivých čtverců a potom už jen dopočítáme obvody. Pozor na jednotky.
-
Otázka 4 / 10
4. Otázka
Záhon tvaru květiny má ve svém středu jezírko. Kolik gramů semene trávy musí zahradníci nakoupit, aby rostla na celém záhonu? Na \(400\:dm^{2}\) je potřeba 0,25 kg trávy.
Počítej na 2 desetinná místa.
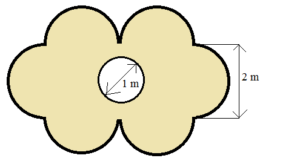Správně
Špatně
Obrazec je vhodné rozdělit na části, které umíme spočítat. Potřebujeme vysadit trávu, budeme počítat obsah.
Obrazec můžeme rozdělit na obdélník se stranami průměr kruhu a dvakrát průměr kruhu. Dále nám tam vyjde 6 polokružnic, což nám dá 3 celé kružnice. Obsah obdélníku a kružnic sečteme, odečteme obsah jezírka. Dostaneme celkovou plochu. Abychom zjistili, kolik gramů trávy potřebujeme, podělíme plochu zadaným obsahem a výsledek vynásobíme množstvím potřebné trávy.
Pozor na jednotky. -
Otázka 5 / 10
5. Otázka
Vypočítej obvod a obsah obrazce, jestliže obsah celého obdélníku je \(32\: j^{2}\). Kratší strana obdélníku je polovinou delší strany obdélníku.
Správně
Špatně
Nejdříve musíme vypočítat rozměry obdélníku. Víme, že jeden je polovinou druhého. Dosadíme do obsahu obdélníku, dostaneme pouze jednu neznámou a umíme dopočítat délky stran. Vykrojené rohy vytváří čtvrtkřužnice. Můžeme spojit a dostaneme půlkruh. Vypočítáme tedy obvod a obsah půlkružnice, tzn. že vzorečky na obvod i obsah kruhu podělíme dvěma.
Obsah obrazce vypočítáme tak, že od obsahu obdélníku odečteme obsah půlkružnice. Obvod obrazce musíme počítat postupně podle délek jednotlivých úseků. -
Otázka 6 / 10
6. Otázka
Obvod hada na obrázku je 56 cm.
Urči, co je správně.
Správně
Špatně
Obvod obrazce můžeme podělit počtem stran malých čtverečků. Dostaneme délku strany čtverce.
Vypočítáme obsah čtverce a vynásobíme počtem čtverců, ze kterých je had složený.
Vypočítáme obvod čtverce.
Hrana je úsečka, ve které se protínají dvě sousední stěny. -
Otázka 7 / 10
7. Otázka
Vypočítej obsah vybarvené části obrazce, jestliže obvod čtverce je 24 j.
Správně
Špatně
Z obvodu čtverce vypočítáme délku strany čtverce. Pokud čtverec rozpůlíme – dostaneme 2 obdélníky, vznikne nám kopule a malé zbytky. Kopule je vlastně půlkruh a pokud máte velkou představivost, vidíte, že ty malé zbytky se nám vejdou mezi kopuli a polovinu čtverce (obdélník).
Pokud to nevidíte, můžete malé zbytky vypočítat tak, že z obsahu obdélníku odečtete obsah půlkruhu – dáte dohromady dvě čtvrtkružnice. -
Otázka 8 / 10
8. Otázka
Kolikrát větší je obsah posledního domečku než prvního?
Jaký je součet všech obvodů domečků?
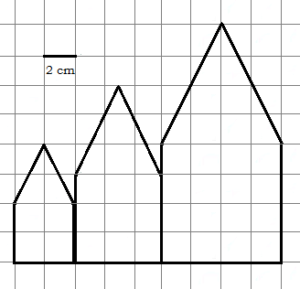Správně
Špatně
Spočítáme obsah prvního a posledního domečku. Obsah posledního domečku podělíme obsahem prvního domečku.
Potřebujeme spočítat obvod jednotlivých domečků, k tomu musíme nejdříve pomocí Pythagorovi věty spočítat délky stran jednotlivých střech. Vzniknou nám tam pomyslné rovnoramenné trojúhelníky.
Dopočítáme a potom už stačí jen správně spočítat jednotlivé obvody domečků.Nápověda
Při výpočtu obvodů využíváme částečné odmocňování.
-
Otázka 9 / 10
9. Otázka
Máme stůl s dřevěnou obdélníkovou deskou o rozměrech 1,5 x 0,5 metru. V každém rohu je zaoblen kružnicí o průměru 20 cm. Kolik metrů čtverečných dřeva je potřeba k výrobě desky stolu?
Správně
Špatně
Máme počítat s metrech čtverečných, tzn., že budeme počítat obsah. Vypočítáme obsah desky stolu. Každý roh je zaoblen čtvrtkružnicí. Když si to nakreslíte, uvidíte, že si obrazec můžete rozdělit na čtvrtkružnice a obdélníky. Budou mít různé rozměry podle odebrané čtvrtkružnice. Všechny čtvrtkružnice dají dohromady celý kruh. Spočítáme tedy jednotlivé obsahy, sečteme a dostaneme výsledek.
-
Otázka 10 / 10
10. Otázka
Obvod kruhu je \(3\pi\: cm\). Obsah \(S_{1}= 15\: cm^{2}\). Jaký je obvod a obsah lichoběžníku? Výsledek zaokrouhli na jedno desetinné místo.
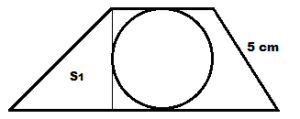Správně
Špatně
Z obvodu kruhu umíme spočítat poloměr (průměr), nemusíte počítat, \(\pi\) se zkrátí – nic neroznásobujte. Díky poloměru (průměru) získáme výšku lichoběžníku a také délku strany c. V pravé části dostáváme pravoúhlý trojúhelník. Umíme pomocí Pythagorovi věty dopočítat třetí stranu. V levé části máme také pravoúhlý trojúhelník. Známe jednu stranu a obsah, dopočítáme stranu. Potom už jen pomocí Pythagorovi věty dopočítáme zbývající stranu. Známe vše pro výpočet obsahu a obvodu lichoběžníku. Dosadíme do vzorečků a máme hotovo.
Povrch a objem hranolů a válce - přijímačky
Procvičení výpočtů povrchů a objemů válce a hranolů s různými typy podstav.
Povrch a objem hranolů a válce - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení výpočtů povrchů a objemů válce a hranolů s různými typy podstav – 10 příkladů.
Můžete při výpočtech využívat kalkulačku. Za \(\pi\) vždy dosazujte 3,14.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Napájecí žlab pro skot má tvar poloviny válce s délkou 2 m a šířkou 80 cm. Jaký je objem žlabu?
Správně
Špatně
Budeme počítat objem válce a výsledek podělíme dvěma.
Šířka žlabu je průměr podstavy a délka je výška válce.
Pozor na jednotky! -
Otázka 2 / 10
2. Otázka
Kašna, která má tvar válce s průměrem podstavy 3 m, je hluboká 70 cm. Kolik hl vody se do ní vejde? Výsledek zaokrouhli na jedno desetinné místo.
Správně
Špatně
Spočítáme objem válce, hloubka kašny je výška válce.
Dáme pozor na jednotky. -
Otázka 3 / 10
3. Otázka
Kvádr je vysoký 6 m, a podstava má strany 500 cm a 40 dm. Je naplněn vodou do výšky 3 m. Kvádr otočíme a jeho podstava bude mít rozměry 4 m a 60 dm. Do jaké výšky bude sahat voda?
Správně
Špatně
Musíme nejdřív vypočítat objem vody, která je v kvádru. Výška kvádru nás pro tento výpočet nezajímá, protože víme, že voda sahá pouze do výše 3 metrů. Proto budeme ve vzorci pracovat s tímto číslem.
Kvádr se nám potom přetočí na jinou podstavu, ale objem vody zůstává stejný. Dosadíme tedy za objem a dvě strany, dopočítáme stranu třetí. To bude naše požadovaná výška.
Pozor na jednotky. -
Otázka 4 / 10
4. Otázka
Za odvoz 10 metrů krychlových zeminy si dopravce účtuje 20 Kč. Kolik zaplatíme za odvoz zeminy z příkopu, který je dlouhý 400 m a příčný řez má tvar rovnoramenného lichoběžníku? Základny lichoběžníku jsou 2 m a 800 cm, délka ramene je 50 dm.
Správně
Špatně
Příkop si můžeme představit jako hranol s podstavou rovnoramenného lichoběžníku. Odváží se metry krychlové, znamená to tedy, že budeme počítat objem. Dosadíme do vzorečku pro objem hranolu a zjistíme, že musíme ještě spočítat výšku podstavy. K tomu využijeme Pythagorovu větu.
Spočítáme objem, podělíme počtem zeminy, a vynásobíme částkou, kterou si dopravce účtuje. -
Otázka 5 / 10
5. Otázka
Vypočítej povrch a objem pravidelného trojbokého hranolu s podstavnou hranou 4 dm. Výška hranolu je 0,6 dm. Jaká je hmotnost hranolu, jestliže je vyroben ze skla o hustotě 4\(\nobreakspace\)100 \(kg\cdot m^{-3}\)?
Výsledky zaokrouhlujte na 2 desetinná místa.Správně
Špatně
Povrch se skládá z výpočtu obsahu podstavy a pláště. Podstavou je rovnostranný trojúhelník, díky tomu umíme pomocí Pythagorovi věty spočítat výšku podstavy a obsah. Obsah pláště spočítáme pomocí obvodu podstavy a vynásobíme výškou hranolu. Obsahy sečteme, podstavy jsou dvě, a máme povrch hranolu.
Objem vypočítáme pomocí vzorce. Využíváme již dříve spočítaný obsah podstavy.
Hmotnost spočítáme pomocí fyzikálního vzorce – objem vynásobený hustotou. Objem jsme již spočítali, vynásobíme hustotou ze zadání.
Dáme pozor na jednotky!Nápověda
-
Otázka 6 / 10
6. Otázka
Jaká je délka podstavné hrany pravidelného čtyřbokého hranolu, jehož objem je \(0,306\:l\) a výška je 85 mm?
Správně
Špatně
Máme pravidelný čtyřboký hranol, tzn., že podstavou je čtverec. Známe objem hranolu, dosadíme do vzorce a dostaneme jednu neznámou. Spočítáme a získáme délku strany čtverce. Pozor na jednotky!
-
Otázka 7 / 10
7. Otázka
Hrnec je do 2/3 naplněn vodou. Dno má obsah \(250\:cm^{2}\). Do hrnce přilijeme 0,035 hl vody. O kolik cm stoupne hladina vody v hrnci?
Správně
Špatně
Známe objem vody, která se do hrnce přidala a také známe obsah podstavy. Dosadíme do vzorečku pro objem a spočítáme výšku. Výsledná výška je i odpovědí na naši otázku.
To, že už v hrnci voda byla a do jaké výšky sahala, nás vůbec nezajímá. -
Otázka 8 / 10
8. Otázka
Kolik plechu je potřeba na výrobu 61 kusů okapových rour o poloměru 22 cm a délce 7 m? Na zahnutí plechu připočítejte 8% materiálu.
Mezivýsledek zaokrouhluj na 2 desetinná místa, konečný výsledek na jedno.Správně
Špatně
Okapovou rourou myslíme okap (rynu). Tzn. polovinu válce z každé strany ukončenou polovinou kruhu.
Chceme zjistit materiál, budeme tedy počítat povrch. Vypočítáme obsah podstavy a nemusíme ji půlit ani násobit, protože na každém konci máme půl kruhu a z toho dostaneme jeden celý kruh. Dále spočítáme obsah pláště a ten podělíme dvěmi. Obsahy sečteme a vynásobíme počtem rour.
Nezapomeneme, např. pomocí trojčlenky, přičíst 8% materiálu navíc. -
Otázka 9 / 10
9. Otázka
Hranol s kosočtvercovou podstavou má jednu úhlopříčku podstavy 6 cm a délku hrany podstavy 50 mm. Výška hranolu je 0,6 dm. Jaký je objem hranolu?
Správně
Špatně
Abychom mohli vypočítat obsah kosočtverce, musíme znát délku druhé úhlopříčky. Víme, že úhlopříčky se vzájemně půlí a jsou na sebe kolmé. Můžeme si tedy vytvořit pravoúhlý trojúhelník, kde známe délku strany kosočtverce, polovinu úhlopříčky a dopočítáme druhou. Potom pomocí úhlopříček spočítáme obsah podstavy. Ten pak už jen vynásobíme výškou hranolu a dostaneme objem.
Pozor na jednotky. -
Otázka 10 / 10
10. Otázka
Vypočtěte obsah plášťě a objem hranolu, jehož podstavou je rovnoramenný pravoúhlý trojúhelník s přeponou délky 16 cm. Výška hranolu je 8 cm.
Výsledek zaokrouhli na celá čísla.Správně
Špatně
Pomocí Pythagorovi věty dopočítáme délky stran trojúhelníku. Víme, že je rovnoramenný, proto budou obě ramena stejně dlouhá. Vypočítáme obsah podstavy a vynásobíme výškou hranolu, dostaneme požadovaný objem.
Potom stačí vypočítat obvod podstavy, vynásobit výškou hranolu a dostaneme obsah pláště.
Derivace II - složené
Procvičení ke složitějším derivacím.
Derivace II - složené
Derivace II – složené
Závěrečný přehled
Zodpovězeno 0 z 9 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
Information
Procvičení ke složitějším derivacím.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 9 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 9
1. Otázka
Bodové ohodnocení: 1Vypočítejte derivaci funkce: \(f(x)=e^{\sqrt {lnx}}\\\)
Správně
Špatně
-
Otázka 2 / 9
2. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=arcsin \dfrac {x-2}{2}\)
Správně
Špatně
-
Otázka 3 / 9
3. Otázka
Bodové ohodnocení: 1Zderivujte funkci \(f(x)=e^{-2x}\cdot sinx-ln(3x^4+5x)\)
Správně
Špatně
-
Otázka 4 / 9
4. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=\dfrac{sinx+cosx}{sinx-cosx}\)
Správně
Špatně
-
Otázka 5 / 9
5. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=\dfrac{3x^3-2^x}{tgx}\)
Správně
Špatně
-
Otázka 6 / 9
6. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=arcsin \dfrac{1}{x}\)
Správně
Špatně
-
Otázka 7 / 9
7. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=\sqrt{ln(1-e^{2x})}\)
Správně
Špatně
-
Otázka 8 / 9
8. Otázka
Bodové ohodnocení: 1Zderivujte funkci:\(f(x)={(x^2+1)}^{sinx}\)
Správně
Špatně
-
Otázka 9 / 9
9. Otázka
Bodové ohodnocení: 1Zderivujte funkci: \(f(x)=\left|x^2-9\right|+9\)
Správně
Špatně
Nerovnice - přijímačky
Procvičení lineárních nerovnic – 10 otázek.
Nerovnice - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení lineárních nerovnic – 10 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vyřeš nerovnici
\(0,5(7-x)-3≤0,2(3+4x)-4\)Správně
Špatně
Roznásobíme závorky, členy s neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 2 / 10
2. Otázka
Vyřeš nerovnici
\(-2[4-(3y-2)]+5[3y+2(1-y)]>0\)Správně
Špatně
Roznásobíme závorky, začínáme od vnitřní po vnější. Členy s neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 3 / 10
3. Otázka
Vyřeš nerovnici
\(\dfrac{2x-1}{2}+2<\dfrac{x+2}{3}-3\)Správně
Špatně
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 4 / 10
4. Otázka
Urči všechna celá kladná čísla, která jsou řešením nerovnice
\(\dfrac{15a-4}{2}<1+6a\)Správně
Špatně
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 5 / 10
5. Otázka
Vyřeš nerovnici
\(4(x^{2}+1)+8(3x-4)>4x^{2}\)Správně
Špatně
Roznásobíme závorky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Neznámou s mocninou by se nám měla vyrušit. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 6 / 10
6. Otázka
Pro \(z\in N<6 \) vyřeš nerovnici
\(1+\dfrac{4}{3}z≥0,5z+3\)Správně
Špatně
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval.
Výsledek máme ze zadání omezen pouze na přirozená čísla, tj. čísla celá kladná – 1, 2, 3, 4, …… Výsledek tedy nebude interval, ale množina čísel. -
Otázka 7 / 10
7. Otázka
Vyřeš nerovnici
\(5(x-1)-x(7-x)<x^{2}≥(x+2)^{2}-6x\)Správně
Špatně
V nerovnici máme dvě znaménka nerovnosti. Musíme tedy řešit postupně dvě nerovnice. Vybereme si např. levou stranu s prostřední, vypočítáme výsledek. Potom si vezmeme prostřední část nerovnice s pravou stranou. Opět vypočítáme výsledek.
Oba výsledky dáme dohromady a konečným výsledkem je průnik.
Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 8 / 10
8. Otázka
Vyřeš nerovnici
\(1,2x+3≤\dfrac{2x}{3}+4<\dfrac{x}{6}-3\)Správně
Špatně
V nerovnici máme dvě znaménka nerovnosti. Musíme tedy řešit postupně dvě nerovnice. Vybereme si např. levou stranu s prostřední, vypočítáme výsledek. Potom si vezmeme prostřední část nerovnice s pravou stranou. Opět vypočítáme výsledek.
Oba výsledky dáme dohromady a konečným výsledkem je průnik.
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 9 / 10
9. Otázka
Vyřeš nerovnici
\(\dfrac{3x-1}{-4}<8+\dfrac{x+3}{6}≥0\)Správně
Špatně
V nerovnici máme dvě znaménka nerovnosti. Musíme tedy řešit postupně dvě nerovnice. Vybereme si např. levou stranu s prostřední, vypočítáme výsledek. Potom si vezmeme prostřední část nerovnice s pravou stranou. Opět vypočítáme výsledek.
Oba výsledky dáme dohromady a konečným výsledkem je průnik.
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen. -
Otázka 10 / 10
10. Otázka
Vyřeš nerovnici
\(\dfrac{5u+4}{2}≤\dfrac{2u+3}{5}>\dfrac{2(3u+2)-3}{4}\)Správně
Špatně
V nerovnici máme dvě znaménka nerovnosti. Musíme tedy řešit postupně dvě nerovnice. Vybereme si např. levou stranu s prostřední, vypočítáme výsledek. Potom si vezmeme prostřední část nerovnice s pravou stranou. Opět vypočítáme výsledek.
Oba výsledky dáme dohromady a konečným výsledkem je průnik.
V nerovnici máme zlomky. Postupujeme stejně jako u klasických rovnic. Nerovnici vynásobíme společným násobkem a díky tomu odstraníme zlomky. Členy neznámou převedeme na jednu stranu, čísla na druhou. Při přechodu přes znaménko nerovnosti měníme znaménka. Výsledek musí být vždy jedna kladná neznámá. V případě, že rovnici násobíme/dělíme znaménkem mínus, otáčí se znaménko nerovnosti.
Výsledkem nerovnice je interval. Pokud je v nerovnici znaménko rovnosti, interval bude z části uzavřen.
Kurz k přijímačkám - Procvičování
Vyzkoušejte, jak byste uspěli u přijímacích zkoušek, kdybyste je měli psát právě teď.
Kurz k přijímačkám - Procvičování
Závěrečný přehled
Zodpovězeno 0 z 14 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
Vyzkoušejte, jak byste uspěli u přijímacích zkoušek, kdybyste je měli psát právě teď.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 14 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 14
1. Otázka
Vyřeš nerovnici
\(\dfrac{5u+4}{2}≤\dfrac{2u+3}{5}>\dfrac{2(3u+2)-3}{4}\)Správně
Špatně
Nerovnice musíme řešit postupně, nejdříve levý a prostřední zlomek, a zvlášť prostřední a pravý zlomek. Vzniknou nám dvě nerovnice.
Počítáme stejně, jakoby tam bylo znaménko rovnosti – odstraníme zlomky (vynásobíme společným jmenovatelem), vyjádříme neznámou a výsledkem bude interval, protože máme nerovnost. Stejně postupujeme u druhé části příkladu. Konečné intervaly dáme do průniku a máme řešení.
-
Otázka 2 / 14
2. Otázka
Vyřeš rovnici:
\( \dfrac{y}{2}\cdot \dfrac{3}{2}-\dfrac{1}{6}y=\dfrac{2}{3}-\dfrac{y}{2}\)Správně
Špatně
V rovnici máme zlomky, můžeme zlomek rovnou odstranit (vynásobíme společným jmenovatelem) anebo si nejdříve upravíme zlomky, které se mezi sebou násobí. Pokud zlomky násobíme, musíme to brát jako jeden člen. V případě odstranění zlomků hned na začátku se v tomto dělá největší problém, protože se součin zlomků musí vynásobit jako jeden celek.
Neznámou dáme na jednu stranu, čísla na druhou a spočítáme.
-
Otázka 3 / 14
3. Otázka
Do odborného učiliště chodí 850 žáků. V pololetí mělo 221 žáků vyznamenání a 18 % žáků mělo jednu nedostatečnou.
A) Kolik žáků mělo jednu nedostatečnou?
B) Kolik procent žáků nemělo vyznamenání ani nedostatečnou?
Správně
A) Víme, že 18% žáků školy mělo nedostatečnou. 100% je 850 žáků a potřebujeme spočítat těch 18%. Využijeme na výpočet buď trojčlenku anebo přes 1%.
B)Zjistíme, kolik žáků mělo nedostatečnou a přičteme žáky, kteří měli vyznamenání. Vypočítáme, kolik je to procent z celku a protože chceme žáky, kteří neměli vyznemenání a nedostatečnou, tak vypočítané procento odečteme od základu.
Anebo od celkového počtu žáků odečteme počet žáků, kteří měli vyznamenání a nedostatečnou. Vypočítáme, kolik je to procent z celku a máme konečný výsledek.
Špatně
-
Otázka 4 / 14
4. Otázka
Ze 3 tun cukrovky se vyrobí 480 kg cukru. Kolik tun cukru se vyrobí ze 17,5 tuny cukrovky?
Správně
Špatně
Jedná se o přímou úměru, protože čím víc cukrovky máme, tím víc cukru získáme. Sestavíme a spočítáme.
-
Otázka 5 / 14
5. Otázka
Na 3 porce zapečených brambor potřebujeme:
– půl kila brambor
– 1/4 kila masa
– 750 ml mléka
– sůl
– kořeníKolik gramů brambor, kilo masa a litrů mléka budeme potřebovat na 5 porcí?
Zaokrouhlujeme až konečné výsledky podle normy!Správně
Špatně
Rozpis je na 3 porce, musíme zjistit rozpis na jednu porci a vynásobit 5, protože chceme pět porcí. Dáváme pozor na jednotky.
-
Otázka 6 / 14
6. Otázka
Za odvoz 10 metrů krychlových zeminy si dopravce účtuje 20 Kč. Kolik zaplatíme za odvoz zeminy z příkopu, který je dlouhý 400 m a příčný řez má tvar rovnoramenného lichoběžníku? Základny lichoběžníku jsou 2 m a 800 cm, délka ramene je 50 dm.
Správně
Špatně
Potřebujeme spočítat objem hranolu. Počítá se jako součin obsahu podstavy a výšky hranolu. Podstavouo je rovnostranný lichoběžník, kde si umíme spočítat jeho výšku. Spočítáme obsah podstavy. Víme, že cena je za 10 metrů krychlových, objem tedy musíme nejdřív vydělit a poté teprve vynásobit cenou. Dáváme pozor na jednotky.
-
Otázka 7 / 14
7. Otázka
Napájecí žlab pro skot má tvar poloviny válce s délkou 2 m a šířkou 80 cm. Jaký je objem žlabu?
Správně
Špatně
Objem válce spočítáme jako součin obsahu podstavy a výšky/délky válce. A protože je to jen polovina, výsledný objem podělíme dvěma.
-
Otázka 8 / 14
8. Otázka
V podniku na výrobu počítačů je zaměstnáno celkem 1 188 pracovníků. Vývojových pracovníků je 540 a zbytek tvoří výrobní pracovníci. V jakém poměru jsou počty vývojových a výrobních pracovníků?
Správně
Špatně
Vypočítáme, kolik je výrobník pracovníků a dáme tyto počty do poměru. Poměr krátíme, až se dostaneme k nějakému rozumnému výsledky nebo do doby, kdy už nelze krátit. Musíme dát pozor na pořadí poměru, nesmíme přehodit pracovníky.
-
Otázka 9 / 14
9. Otázka
Urči měřítko mapy, na které je vzdálenost 1,04 km znázorněna úsečkou v délce 52 mm.
Správně
Špatně
Měřítko získáme tak, že dáme do poměru vzdálenost na mapě a skutečnou vzdálenost. Musíme mít stejné jednotky. Poměr upravujeme tak dlouho, dokud nezískáme měřítko jednu ku něčemu (1: ….)
-
Otázka 10 / 14
10. Otázka
Vypočítej obvod a obsah obrazce, jestliže obsah celého obdélníku je \(32\: j^{2}\). Kratší strana obdélníku je polovinou delší strany obdélníku.
Správně
Špatně
V obrazci můžeme vidět obdélník. Obsah vypočítáme jako součin dvou stran. Víme, že jedna je polovinou druhé, protože můžeme napsat, že strana a = 2b. Dosadíme do vzorce a zůstaneme nám pouze jedna neznámá. Díky tomu dopočítáme délky stran. Vyřízlé části dají dohromady půlkruh.
Obvod spočítáme postupně – napočítáme, jak dlouhé jsou zbylé strany a přičteme polovinu obvodu kruhu.
Obsah spočítáme tak, že od obsahu obdélníku odečteme polovinu obsahu kruhu. -
Otázka 11 / 14
11. Otázka
Uprav a výsledek uveď bez závorek:
\(8(a^2-4a)+(a-3)(2a+4)\)Správně
Špatně
Odstraníme závorky – první závorku roznásobíme pouze číslem, součin závorek musíme násobit každý člen první závorky každým členem druhé závorky. Členy se stejným základem a exponentem můžeme sečíst/odečíst.
-
Otázka 12 / 14
12. Otázka
Navštívili jsme čokoládovnu a mícháme si bonbony. Na výběr jsou dva druhy. První druh stojí 180 Kč/kg a druhý druh stojí 210 Kč/kg. Chceme si koupit 25 kg čokoládových bonbonů v ceně 192 Kč za 1 kg směsi. Kolik kilo jakého druhu čokolády koupíme?
Správně
Špatně
Slovní úlohu je dobré řešit soustavou rovnic. Ze zadání hned vyplynou dvě neznámé, které v druhé rovnici přenásobíme korunami za kilo. Soustavu řešíme metodou sčítací nebo dosazovací. Spočítáme hodnotu jedné neznámé a díky tomu dopočítáme i druhou neznámou.
-
Otázka 13 / 14
13. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac {3}{5}^{2}-\dfrac {3}{5^{2}}+{\left(-\dfrac {3}{5}\right)^{2}}\)Správně
Špatně
Dáme pozor, která část zlomku je na mocninu. Zápor na kladnou mocninu nám dá kladný výsledek. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a pracujeme s čitatelem. Nezapomínáme krátit.
-
Otázka 14 / 14
14. Otázka
Vypočítej:
\(64:8\cdot2-25:(5\cdot0-5\cdot1)\)Správně
Špatně
Dáváme pozor na to, co má přednost – závorky, násobení/dělení a sčítání/odčítání.
Logaritmus I.
Procvičení použití definice logaritmů – 10 příkladů.
Logaritmus I.
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení použití definice logaritmů – 10 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej dané neznámé:
a) \( log_{\frac {2}{5}}{\frac {25}{4}}=y \)b) \( log_a{\frac {3}{4}}=-1\)
c) \( log_6{x}=3 \)
Správně
Špatně
-
Otázka 2 / 10
2. Otázka
Vypočítej
\( log_{5}125-log_4{x}=9\)Správně
Špatně
-
Otázka 3 / 10
3. Otázka
Vypočítej
\( log_2{2}+logx=4\)Správně
Špatně
-
Otázka 4 / 10
4. Otázka
Vypočítej
\( log_9{81}+log_2{16} \)Správně
Špatně
-
Otázka 5 / 10
5. Otázka
Vypočítej
\( log_5{\dfrac {1}{125}}+3log_{\frac {1}{2}}{\dfrac {1}{32}} \)Správně
Špatně
-
Otázka 6 / 10
6. Otázka
Vypočítej
\( log_4{(log_2{16})}+3log_2{(log_2{2})}\)Správně
Špatně
-
Otázka 7 / 10
7. Otázka
Vypočítej
\( log_{\sqrt{5}}{625}-log_{\sqrt[3]{4}}{32}=log_{9}x\)Správně
Špatně
-
Otázka 8 / 10
8. Otázka
Vypočítej
\( log_{9}{\frac {1}{27}}+log_{\sqrt[3]{216}}{1}=log_{4}x\)Správně
Špatně
-
Otázka 9 / 10
9. Otázka
Vypočítej dané neznámé:
a) \( log_{1,5}{\sqrt[7]{\frac {8}{27}}}=y \)b) \( log_a{\sqrt{\frac {1}{343}}}=-\frac {3}{2}\)
c) \( log_{\frac {1}{6}}{x}=\frac {3}{5} \)
Správně
Špatně
-
Otázka 10 / 10
10. Otázka
Vypočítej
\(2 log_{\sqrt{3}}{\frac {1}{27}}-3log_{\frac {1}{4}}{256}+log_{\sqrt[4]{2}}{64} \)Správně
Špatně
Logaritmus II.
Procvičení používání vět pro logaritmy – 15 příkladů.
Logaritmus II.
Závěrečný přehled
Zodpovězeno 0 z 15 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Procvičení používání vět pro logaritmy – 15 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 15 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 15
1. Otázka
Zlogaritmuj daný výraz
\(\dfrac {(a+b)^{2}}{\sqrt{xy}}\)Správně
Špatně
-
Otázka 2 / 15
2. Otázka
Zlogaritmuj daný výraz
\(\dfrac {100^{2}\cdot 0,1^{3}}{\sqrt[4]{1\:000}\cdot \sqrt{10}}\)Správně
Špatně
-
Otázka 3 / 15
3. Otázka
Zlogaritmuj daný výraz
\(\dfrac {x\sqrt[3\:]{y}}{y\sqrt[4\:]{x}}\)Správně
Špatně
-
Otázka 4 / 15
4. Otázka
Zlogaritmuj daný výraz
\(\dfrac {\sqrt{\dfrac{a}{b}}}{\sqrt[3\:]{\dfrac{b^2}{a^2}}}\)Správně
Špatně
-
Otázka 5 / 15
5. Otázka
Zlogaritmuj daný výraz
\(\sqrt{\dfrac {x+1}{x-1}}\cdot\sqrt[3\:]{\dfrac{2x^2}{x^3+8}}\)Správně
Špatně
-
Otázka 6 / 15
6. Otázka
Odlogaritmuj daný výraz
\(3log_{\:}m-log_{\:}n-log_{\:}p\)Správně
Špatně
-
Otázka 7 / 15
7. Otázka
Určete výraz, jehož logaritmováním dostaneme
\(log_{\:}a+\dfrac {1}{3}log_{\:}b-log_{\:}c-\dfrac {3}{4}log_{\:}d\)Správně
Špatně
-
Otázka 8 / 15
8. Otázka
Určete výraz, jehož logaritmováním dostaneme
\(3log_{10}n-4log_{10}(n+1)+2\)Správně
Špatně
-
Otázka 9 / 15
9. Otázka
Odlogaritmuj výraz
\(log_{\:}2+log_{\:}\pi+\dfrac {1}{2}log_{\:}l-\dfrac {1}{2}log_{\:}3-\dfrac {1}{2}log_{\:}g\)Správně
Špatně
-
Otázka 10 / 15
10. Otázka
Odlogaritmuj výraz
\(6log_{4}(4-x)-3-log_{4}x\)Správně
Špatně
-
Otázka 11 / 15
11. Otázka
Vypočítej hodnotu výrazu
\(4log_{6}3+5log_{6}2-log_{6}12\)Správně
Špatně
-
Otázka 12 / 15
12. Otázka
Vypočítej
\(log_{0,5}6+log_{0,5}\dfrac {4}{6}\)Správně
Špatně
-
Otázka 13 / 15
13. Otázka
Řeš logaritmicky
\(x=\dfrac {1}{\pi}\cdot \left(\dfrac {1,354}{0,8735}\right)^3\)Správně
Špatně
-
Otázka 14 / 15
14. Otázka
Řeš logaritmicky
\(x=\dfrac {\sqrt[7\:]{0,374^3}}{\sqrt[5\:]{216^4}}\)Správně
Špatně
-
Otázka 15 / 15
15. Otázka
Řeš logaritmicky
\(x=\sqrt[3\:]{\dfrac {0,365 \cdot \sqrt{2}}{788}}\)Správně
Špatně
Popisná statistika
Procvičení příkladů z kurzu Popisná statistika.
Popisná statistika
Závěrečný přehled
Zodpovězeno 0 z 8 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Information
Procvičení příkladů z kurzu Popisná statistika. V testu Vás čekají příklady na výpočet průměru, mediánu a rozptylu.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 8 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 8
1. Otázka
Bodové ohodnocení: 6Je dána tabulka rozdělení četností. Vypočítejte aritmetický průměr, geometrický i harmonický průměr. Dále spočítejte medián a modus.
\(
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline
i & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\
\hline
x_i & 3 & 5 & 6 & 7 & 8 & 10 & 11 & 13\\
\hline
n_i & 5 & 3 & 8 & 7 & 10 & 11 & 4 & 2\\
\hline
\end{array}
\)-
Aritmetický průměr je (7,74).
Geometrický průměr je (7,26).
Harmonický průměr je (6,696).
Medián je (8).
Modus je (10).
Správně
Špatně
Aritmetický průměr vypočítáte podle vzorečku:
$$
\overline{x}=\dfrac{\sum_{i=1}^k x_i\cdot n_i}{\sum_{i=1}^k n_i}
$$ -
-
Otázka 2 / 8
2. Otázka
Bodové ohodnocení: 1Čtyři brigádnice za jedno dopoledne nasbírali 32 košíků jahod. Vypočítejte průměrnou váhu košíku, víte-li že první brigádnice nasbírala 8 košíků s průměrnou váhou 2 850 g, druhá brigádnice 9 košíků s průměrnou váhou 2 700 g, třetí brigádnice 6 košíků s průměrnou váhou 2 800 g a čtvrtá brigádnice 9 košíků s průměrnou váhou 2 870 g.
Správně
Špatně
Využijte vzoreček
$$
\overline{x}=\dfrac{x_1+…+x_{32}}{32}
$$ -
Otázka 3 / 8
3. Otázka
Bodové ohodnocení: 1Řidič automobilu jel z Opavy do Ostravy rychlostí 85 km/h. Na zpáteční cestě jel rychlostí 70 km/h. Jakou průměrnou rychlostí řidič jel na celé trase?
Pozn. Výsledek zaokrouhlete na 2 desetinná místa.Správně
Špatně
Použijte vzoreček na výpočet harmonického průměru:
$$
\overline{x}_H=\dfrac{n}{\sum{} \dfrac{1}{x_i}}
$$ -
Otázka 4 / 8
4. Otázka
Bodové ohodnocení: 1Supermarket má na víkend nachystáno k prodeji 500 ks krůt s průměrnou váhou 6,8 kg za akční cenu 80 Kč/kg. V sobotu se prodalo 200 ks krůt za 120 000 Kč. Jaká je průměrná váha neprodaných krůt?
Pozn. výsledek zaokrouhlete na 2 desetinná místa.Správně
Špatně
Nejprve spočítejte celkovou hmotnost prodaných krůt: \(\dfrac{120000}{80}=1500\).
Pak použijte vzoreček pro výpočet průměrné hodnoty:
$$
\dfrac{x_1+…+x_{200}+x_{201}+…+x_{500}}{500}=6,8\\
\dfrac{1500+x_{201}+…+x_{500}}{500}=6,8\\
x_{201}+…+x_{500}=1900\\
\overline{x}_n=\dfrac{x_{201}+…+x_{500}}{300}=\dfrac{1900}{300}=\underline{\underline{6,33}} \text{ kg}
$$ -
Otázka 5 / 8
5. Otázka
Bodové ohodnocení: 12V tabulce najděte nejnižší a nejvyšší měsíční náklady v Kč na dojíždění za prací. Vypočítejte variační rozpětí, kvartily, kvartilové rozpětí a modus.
$$
\begin{array}{ccccc}
i & x_i & \text{} & i & x_i \\
\hline
1 & 550 & \text{} & 11 & 300 \\
2 & 320 & \text{} & 12 & 650 \\
3 & 540 & \text{} & 13 & 900 \\
4 & 500 & \text{} & 14 & 250 \\
5 & 560 & \text{} & 15 & 200 \\
6 & 350 & \text{} & 16 & 450 \\
7 & 150 & \text{} & 17 & 320 \\
8 & 100 & \text{} & 18 & 1490 \\
9 & 860 & \text{} & 19 & 1500 \\
10 & 1200 & \text{} & 20 & 600
\end{array}
$$-
Nejnižší měsíční náklady na dojíždění do práce jsou ve výši (100) Kč a naopak nejvyšší jsou (1500) Kč.
Variační rozpětí je (1400) Kč.
Dolní kvartil (25% kvantil) je (310) Kč.
Medián (50% kvantil) je (520) Kč.
Horní kvantil (75% kvantil) je (755) Kč.
Kvartilové rozpětí je (445) Kč.
Modus je (320) Kč.
Správně
Špatně
Nejdříve si částky za dopravu seřaďte vzestupně podle velikosti (od nejmenší po největší).
Variační rozpětí je \(R=x_{max}-x_{min}\).
Pro výpočet kvartilů použijte vzoreček: \(n\cdot \dfrac{p}{100}\le m_p \le n\cdot \dfrac{p}{100}+1\).
Kvartilové rozpětí je rozdíl 3. kvartilu a 1. kvartilu (75% kvantilu a 25% kvantilu).
Modus je nejčetnější hodnota. -
-
Otázka 6 / 8
6. Otázka
Bodové ohodnocení: 1Průměrný věk zaměstnanců poklesl o 15 %, přičemž rozptyl se zvýšil 21 %. Jak se změnil variační koeficient?
Správně
Špatně
Vyjděte ze vzorečku \(V_x=\dfrac{s_x}{\overline{x}}\).
Nový průměr je 85 % původního průměru a rozptyl je 121 % původního rozptylu. Dosaďte do vzorečku tyto hodnoty a dostanete:
$$
V_n=\dfrac{0,85\overline{x}}{1,1s}
$$ -
Otázka 7 / 8
7. Otázka
Bodové ohodnocení: 1U 500 osob byl zjištěn jejich věk. Ze získaných údajů vyplynulo, že průměr věk všech osob je 32 let, směrodatná odchylka 4 roky a variační koeficient 12,5 %. Jak se změní uvedené charakteristiky za 8 let?
- Za 8 let průměrný věk sledovaných osob bude (40) let. Směrodatná odchylka bude (4) roky/let a variační koeficient bude (10) %.
Správně
Špatně
Využijte vlastností průměru a směrodatné odchylky. Přičtením stejné hodnoty všem osobám se i průměr zvýší o stejnou hodnotu, směrodatná odchylka zůstane stejná. A variační koeficient se spočítá podle vzorečku \(V_x=\dfrac{s}{\overline{x}}\).
-
Otázka 8 / 8
8. Otázka
Bodové ohodnocení: 1V následující tabulce jsou údaje o 30 domácnostech. Proměnná \(x_1\) značí měsíční výdaje domácnosti na potraviny v Kč, proměnná \(x_2\) počet členů domácnosti, proměnná \(x_3\) měsíční příjem domácnosti v Kč, proměnná \(x_4\) počet dětí a proměnná \(x_5\) vlastnictví automobilu.
1) Určete typ uvedených proměnných.
2) Sestavte tabulku rozdělení absolutních, relativních a kumulativních četností počtu dětí.
3) Najděte nejnižší a nejvyšší měsíční výdaje domácností na potraviny.
4) Vypočítejte variační rozpětí, kvartily a kvartilové rozpětí měsíčních výdajů domácností na potraviny.
5) Vypočítejte průměrnou hodnotu, rozptyl a směrodatnou odchylku měsíčního příjmů domácností.$$
\begin{array}{cccccc}
i & x_1 & x_2 & x_3 & x_4 & x_5 \\
\hline
1 & 12 045 & 4 & 50 230 & 2 & \text{ano}\\
2 & 6 300 & 2 & 36 900 & 0 & \text{ne}\\
3 & 8 760 & 3 & 25 450 & 1 & \text{ano}\\
4 & 11 430 & 3 & 46 840 & 1 & \text{ano}\\
5 & 10 670 & 3 & 68 340 & 0 & \text{ano}\\
6 & 4 500 & 1 & 20 560 & 0 & \text{ne}\\
7 & 16 560 & 5 & 54 820 & 3 & \text{ne}\\
8 & 8 530 & 4 & 52 340 & 2 & \text{ano}\\
9 & 9 112 & 3 & 37 110 & 2 & \text{ano}\\
10 & 7 459 & 1 & 28 560 & 0 & \text{ano}\\
11 & 17 680 & 5 & 45 120 & 2 & \text{ano}\\
12 & 5 430 & 1 & 35 760 & 0 & \text{ano}\\
13 & 12 439 & 4 & 29 200 & 2 & \text{ano}\\
14 & 8 100 & 2 & 15 700 & 1 & \text{ano}\\
15 & 13 568 & 3 & 32 480 & 1 & \text{ano}\\
16 & 5 465 & 1 & 44 670 & 0 & \text{ano}\\
17 & 6 954 & 2 & 19 360 & 1 & \text{ne}\\
18 & 9 567 & 3 & 26 400 & 0 & \text{ano}\\
19 & 19 211 & 6 & 78 240 & 4 & \text{ano}\\
20 & 8 645 & 3 & 24 600 & 2 & \text{ano}\\
21 & 9 231 & 2 & 26 900 & 1 & \text{ano}\\
22 & 11 549 & 3 & 32 500 & 2 & \text{ano}\\
23 & 12 478 & 4 & 43 500 & 2 & \text{ano}\\
24 & 15 340 & 5 & 42 600 & 3 & \text{ano}\\
25 & 13 649 & 3 & 25 300 & 1 & \text{ano}\\
26 & 9 021 & 2 & 40 000 & 0 & \text{ano}\\
27 & 14 367 & 2 & 19 540 & 0 & \text{ne}\\
28 & 14 213 & 4 & 37 800 & 1 & \text{ano}\\
29 & 22 540 & 6 & 45 600 & 4 & \text{ano}\\
30 & 10 940 & 3 & 52 650 & 1 & \text{ano}\\
\end{array}
$$Správně
Špatně
Logaritmické rovnice
Procvičení výpočtů logaritmických rovnic.
Logaritmické rovnice
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičení výpočtů logaritmických rovnic. Najdete zde rovnice základní, řešené pomocí substituce i rovnice exponenciální, které se řeší pomocí logaritmů.
Procvičení obsahuje 20 otázek.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Vyřeš rovnici
\(log_{2}(x+1)=3\)Správně
Špatně
Na pravé straně rovnice máme číslo 3. Abychom mohli rovnici odlogaritmovat, musíme mít vlevo i vpravo log o stejném základu. Pomocí definice pro logaritmus spočítáme \begin{eqnarray*}log_{a}x=y ⇒ a^y&=&x\\[2ex] log_{2}x&=&3\end{eqnarray*} Poté už jen odlogaritmujeme.
-
Otázka 2 / 20
2. Otázka
Vyřeš rovnici
\(log_{0,1}(x^2-5x)=log_{0,1}(5x+11)\)Správně
Špatně
Vlevo i vpravo máme log o stejném základu, stačí odlogaritmovat a všechny členy převést na jednu stranu rovnice. Dostaneme kvadratickou rovnici a vyřešíme kořeny.
Pozor na podmínky. -
Otázka 3 / 20
3. Otázka
Vyřeš rovnici
\(log_{\:}x=2log_{\:}5+log_{\:}4\)Správně
Špatně
Pravou stranu rovnice upravíme podle vět pro logaritmy. Sčítání nahradíme násobením, člen před log se naopak objeví v exponentu. Jakmile máme jeden log vlevo a jeden log vpravo, odlogaritmujeme a řešíme.
-
Otázka 4 / 20
4. Otázka
Vyřeš rovnici
\(log_{\:}x^5-log_{\:}x^4+log_{\:}x^3=12\)Správně
Špatně
Na levé straně rovnice využijeme věty pro úpravu logaritmů, případně zkrátíme. Vpravo využijeme definici logaritmu, abychom dostali log o stejném základu jako vlevo. Výsledek levé strany nemusíme nutně vyčíslovat. Odlogaritmujeme a případný výsledek odmocníme. Abychom dostali konečný výsledek, vzpomeneme si, jak se dají odmocniny převést na mocniny a naopak.
-
Otázka 5 / 20
5. Otázka
Vyřeš rovnici
\(log_{\:}(x-13)-log_{\:}(x-3)=1-log_{\:}2\)Správně
Špatně
Upravíme rovnici tak, abychom měli na každé straně log. Využijeme věty pro úpravu logaritmů. Odlogaritmujeme a spočítáme.
-
Otázka 6 / 20
6. Otázka
Vyřeš rovnici
\(\dfrac {log_{5}\left(x-\dfrac {1}{4}\right)}{log_{5}\left(x+\dfrac {7}{2}\right)}=-1\)Správně
Špatně
Zbavíme se zlomku provedeme úpravy podle vět pro logaritmus, odlogaritmujeme a upravíme. Dostaneme kvadratickou rovnici, vyjdou nám dva kořeny, které musíme porovnat s podmínkami pro logaritmus.
-
Otázka 7 / 20
7. Otázka
Vyřeš rovnici
\(\dfrac {2+log_{\:}x}{log_{\:}x-3}=3\)Správně
Špatně
Zbavíme se zlomku. Roznásobíme, členy s neznámou dáme na jednu stranu, čísla na druhou. Spočítáme, rovnici můžeme i zkrátit a potom už jen stačí podle definice pro logaritmus dopočítat výsledek.
-
Otázka 8 / 20
8. Otázka
Vyřeš rovnici
\(\dfrac {log_{\:}(2x-5)}{log_{\:}(x^2-8)}=\dfrac {1}{2}\)Správně
Špatně
Zbavíme se zlomku, použijeme věty pro úpravu logaritmů. Odlogaritmujeme a dostaneme závorku na 1/2. To také můžeme zapsat jako odmocninu ze závorky. Rovnici umocníme, vypočítáme a vyjde nám kvadratická rovnice. Zkontrolujeme, jestli oba kořeny vyhovují podmínkám.
-
Otázka 9 / 20
9. Otázka
Vyřeš rovnici
\(\dfrac {log_{\:}[(x+1)^2(x+2)]}{log_{\:}(x+3)}=3\)Správně
Špatně
Rovnici vynásobíme, abychom se zbavili zlomku. Pomocí vět pro logaritmus upravíme pravou stranu rovnice. Rovnici odlogaritmujeme. Roznásobíme závorky, upravíme a dostaneme kvadratickou rovnici. Spočítáme a zjistíme že diskriminant vyjde záporný.
-
Otázka 10 / 20
10. Otázka
Vyřeš rovnici
\(\dfrac {log_{2}(x+3)(x+2)}{log_{2}1}=log_{2}64\)Správně
Špatně
Pravou stranu rovnice umíme vyčíslit pomocí věty pro logaritmus. Rovnici potom vynásobíme tak, aby nám zmizel zlomek. Použijeme další úpravy pro logaritmy. Pokud máme na obou stranách stejné logaritmy, můžeme rovnici odlogaritmovat. Dostaneme kvadratickou rovnici, spočítáme kořeny a ověříme, jestli oba vyhovují podmínkám.
-
Otázka 11 / 20
11. Otázka
Vyřeš rovnici
\(log_{2}x^{2}-log_{2}x=log_{2}4 \)Správně
Špatně
Pravou stranu rovnice umíme převést na číslo. Máme v rovnici mocninu, která nás vede na kvadratickou rovnici. Abychom ji uměli vypočítat, provedeme substituci. Spočítáme nové kořeny a nesmíme zapomenout dosadit do substituce. Zkontrolujeme podmínky a dostáváme řešení.
-
Otázka 12 / 20
12. Otázka
Vyřeš rovnici
\((log_{5}u)^{-1}-2=-log_{5}u\)Správně
Špatně
Logaritmus na -1 převedeme na zlomek. Rovnici vynásobíme tak, abychom se zbavili zlomku. Dostaneme logaritmus na druhou mocninu, uděláme substituci a spočítáme kořeny. Výsledky dosadíme do substituce a zkontrolujeme podmínky.
-
Otázka 13 / 20
13. Otázka
Vyřeš rovnici
\(ln\:x – 1=\dfrac{12}{ln\:x}\)Správně
Špatně
Zbavíme se zlomku, dostaneme kvadratickou rovnici. Uděláme substituci a vypočítáme kořeny. Dosadíme do substituce. Základem přirozeného logaritmu je e. Výsledek nebudeme upravovat. Zkontrolujeme podmínky.
-
Otázka 14 / 20
14. Otázka
Vyřeš rovnici
\((2log_{16}x+1)^{2}=log_{16}x+2\)Správně
Špatně
Levou stranu rovnice upravíme pomocí algebraického vzorce. Dostaneme se ke kvadratické rovnici, uděláme substituci a spočítáme kořeny. Kořeny dosadíme do substituce a vypočítáme řešení. Zkontrolujeme s podmínkami.
-
Otázka 15 / 20
15. Otázka
Vyřeš rovnici
\((log_{\:}x-2)(3log_{\:}x+4)=-7\)Správně
Špatně
Závorky roznásobíme, členy upravíme a dostaneme kvadratickou rovnici. Uděláme substituci, vypočítáme kořeny a dosadíme do substituce. Abychom dostali správné výsledky, musíme při výpočtu jednoho konečného výsledku použítá usměrnění zlomků. Zkontrolujeme podmínky.
-
Otázka 16 / 20
16. Otázka
Vyřeš rovnici
\(3^{2x+1}=5^{x}\)Správně
Špatně
Rovnici nedostaneme na stejný základ, proto ji celou zlogaritmujeme. Při úpravách využijeme věty pro logaritmy. Upravujeme tak dlouho, dokud nemáme členy s neznámou na jedné straně a zbytek na druhé. Vytkneme neznámou, rovnici vyděláme a potom už jen zadáme do kalkulačky.
-
Otázka 17 / 20
17. Otázka
Vyřeš rovnici
\(5^{3-x}=3^{2x-1}\)Správně
Špatně
Rovnici zlogaritmujeme, upravíme podle vět. Neznámou převedeme na jednu stranu, čísla na druhou. Osamostatníme neznámou a výpočet zadáme do kalkulačky.
-
Otázka 18 / 20
18. Otázka
Vyřeš rovnici
\(1=\dfrac{5^{2m+1}}{3^{m-5}}\)Správně
Špatně
Nejdříve se zbavíme zlomku. Rovnici zlogaritmujeme, neznámé dáme na jednu stranu, osamostatníme a dostaneme výsledek.
-
Otázka 19 / 20
19. Otázka
Vyřeš rovnici
\(2^x\cdot 3^{x}=4^{x-1}\)Správně
Špatně
Rovnici zlogaritmujeme, použijeme věty pro výpočet logaritmů. Jakmile budeme mít vše upraveno, dáme neznámou na jednu stranu, čísla na druhou. Neznámou osamostatníme a výsledek zadáme do kalkulačky.
-
Otázka 20 / 20
20. Otázka
Vyřeš rovnici
\(3^{x+2}-7=0\)Správně
Špatně
7 převedeme na druhou stranu rovnice, rovnici zlogaritmujeme, upravíme pomocí vět pro logaritmy a dopočítáme.
Soustava - slovní - přijímačky
Procvičení slovních úloh na soustavu dvou rovnic o dvou neznámých.
Soustava - slovní - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení slovních úloh na soustavu dvou rovnic o dvou neznámých – 10 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Pokladník vyplatil 2 570 Kč 67 bankovkami. Bankovky měly hodnotu 20 Kč a 50 Kč. Kolik kusů musel mít od každé bankovky?
Správně
Špatně
Máme 2 druhy bankovek, tedy 2 neznámé. Např. x a y.
Bankovek měl 67, tzn. že když sečteme obě neznámé, dostaneme celkový počet bankovek. Máme jednu rovnici.
Druhá rovnice se skládá z kusů přenásobených hodnotou, tj. x má hodnotu 20 Kč, proto budeme mít 20x (20 krát počet korun). To samé s druhou neznámou. Sečteme, dáme rovno celkové hodnotě a máme soustavu rovnic.
Počítáme metodou sčítací nebo dosazovací. Abychom uměli odpovědět na otázku, musíme neznámé dosadit do soustavy. -
Otázka 2 / 10
2. Otázka
12 kg polohrubé mouky a 20 kg hladké mouky stálo dohromady 200 Kč. Kilo hladké mouky je o 2 Kč dražší než kilo mouky polohrubé. Kolik korun stojí 1 kg hladké a 1 kg polohrubé mouky?
Správně
Špatně
Máme 2 neznámé, např. x a y. Víme, že vše celkem stálo 200. Máme první rovnici.
Hladká mouka je dražší, ve druhé rovnici se tedy bude jedna neznámá rovnat druhé s tím, že u hladké mouky dáme dražší cenu. Máme sestavenou soustavu a můžeme počítat.
Počítáme metodou sčítací nebo dosazovací. Abychom uměli odpovědět na otázku, musíme neznámé dosadit do soustavy. -
Otázka 3 / 10
3. Otázka
Myslím si číslo, jehož ciferný součet je 12. První číslice je o 2 větší než druhá číslice. Jaké číslo si myslím?
Správně
Špatně
-
Otázka 4 / 10
4. Otázka
Navštívili jsme čokoládovnu a mícháme si bonbony. Na výběr jsou dva druhy. První druh stojí 180 Kč/kg a druhý druh stojí 210 Kč/kg. Chceme si koupit 25 kg čokoládových bonbonů v ceně 192 Kč za 1 kg směsi. Kolik kilo jakého druhu čokolády koupíme?
Správně
Špatně
-
Otázka 5 / 10
5. Otázka
Délku obdélníku zmenšíme o 10 m a šířku obdélníku o 20 m. Obsah obdélníku se zmenší o 1 800 \(m^{2} \). Pokud šířku zmenšíme o 10 m a délku o 20 m, zmenší se obsah o 2 300 \(m^{2} \). Jaké jsou rozměry obdélníku?
Správně
Špatně
-
Otázka 6 / 10
6. Otázka
Vyřeš soustavu:
$$\begin{eqnarray*}2r+s&=&4\\
8r+4s&=&16\\\end{eqnarray*}$$Správně
Špatně
-
Otázka 7 / 10
7. Otázka
Vyřeš soustavu rovnic:
$$\begin{eqnarray*}\dfrac{a+b}{3}-\dfrac{2a}{4}&=&5\\
\dfrac{a-2b}{4}+\dfrac{2a+b}{3}&=&5\\\end{eqnarray*}$$Správně
Špatně
-
Otázka 8 / 10
8. Otázka
Na dvorku se pasou slepice a myši chytají kočky. Zvířat je na dvoře 17 a mají celkem 38 nohou. Kolik je na dvoře slepic a kolik koček?
Správně
Špatně
-
Otázka 9 / 10
9. Otázka
85 studentů střední školy jelo na výlet. Měli zamluvených 19 chat. Chaty jsou pro čtyři nebo pět lidí. Když se studenti ubytovali, zjistili, že 2 lůžka zůstala volná. Kolik čtyř a pěti lůžkových chat studenti obsadili?
Správně
Špatně
-
Otázka 10 / 10
10. Otázka
Maminka koupila na oslavu narozenin špičky a indiány. Hostů bylo 21 a každý dostal jeden zákusek. Za všechny zákusky zaplatila celkem 303 Kč. Kolik korun stála špička?
Správně
Špatně
Mnohočleny - přijímačky
Procvičení sčítání, odčítání a násobení mnohočlenů.
Mnohočleny - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení sčítání, odčítání a násobení mnohočlenů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej:
\(6(c-2d)+3(c-4d)\)Správně
Špatně
Roznásobíme závorky, sčítáme/odčítáme mnohočleny ty, které mají stejnou neznámou a zároveň stejný exponent.
-
Otázka 2 / 10
2. Otázka
Vypočítej
\((2b+5)(3b-4)\)Správně
Špatně
Roznásobíme závorky – každý s každým, tj. první člen první závorky vynásobíme postupně každým členem druhé závorky, to samé uděláme s druhým členem první závorky. Násobíme tak, že čísla mezi sebou a u neznámých základ opíšeme a exponenty sečteme. Zkontrolujeme, jestli se nějaké členy dají sečíst/odečíst.
-
Otázka 3 / 10
3. Otázka
Vypočítej
\((0,1x+0,4y)^2\)Správně
Špatně
Nejdříve spočítáme závorku. Vidíme, že v ní žádné členy nemůžeme sečíst/odečíst. Závorka je na druhou mocninu, musíme použít algebraický vzorec
\((a+b)^2=a^2+2ab+b^2\). -
Otázka 4 / 10
4. Otázka
Rozlož na součin (vytýkání):
\(75c^2d-25cd+50c^2d^2\)Správně
Špatně
Vytýkání můžeme chápat jako dělení. Podíváme se, jestli můžeme vytknout nějaké (nejmenší společný násobek) číslo. Potom se podíváme, jestli máme stejné proměnné a případně můžeme vytknout i na nějakou mocninu. Vytýkáme před závorku, do závorky píšeme „zbytek“.
-
Otázka 5 / 10
5. Otázka
Vypočítej podle vzorců:
\((5+2x)^2\)Správně
Špatně
Nejdříve spočítáme závorku. Vidíme, že v ní žádné členy nemůžeme sečíst/odečíst. Závorka je na druhou mocninu, musíme použít algebraický vzorec
\((a+b)^2=a^2+2ab+b^2\). -
Otázka 6 / 10
6. Otázka
Vypočítej podle vzorců:
\(121-66x+9x^2\)Správně
Špatně
Členy nemůžeme sečíst/odečíst, nemáme ani co vytknout, musíme tedy použít algebraické vzorce.
Víme, že jsou tři typy – dva z nich mají 3 členy, třetí má pouze dva. My máme tři členy, vybíráme tedy vzorec podle znaménka u prostředního členu.
\((a-b)^2=a^2-2ab+b^2\).
Ze vzorce vidíme, že odmocníme první a třetí člen a dáme do závorky na druhou mocninu. Zkontrolujeme, jestli nám vychází prostřední člen. Kdyby nevycházel, příklad bychom neuměli nijak upravit. -
Otázka 7 / 10
7. Otázka
Rozlož na součin činitelů (vytýkání):
\(2(x+y)-a(x+y)\)Správně
Špatně
Závorky by se daly roznásobit, ale k řešení by nám to moc nepomohlo. Navíc máme v zadání, že máme rozložit na součim, což znamená násobení. Můžeme vytknout celou závorku, protože obě jsou stejné. V další závorce nám zůstane „zbytek“.
-
Otázka 8 / 10
8. Otázka
Rozlož na součin činitelů (vytýkání):
\(4a(z+xy)-3b(xy+z)\)Správně
Špatně
Závorky by se daly roznásobit, ale k řešení by nám to moc nepomohlo. Navíc máme v zadání, že máme rozložit na součim, což znamená násobení. Můžeme vytknout celou závorku, protože obě jsou stejné (stačí přehodit uspořádání členů). V další závorce nám zůstane „zbytek“.
-
Otázka 9 / 10
9. Otázka
Rozlož na součin činitelů (podle vzorců):
\(a^8-6a^4b^3+9b^6\)Správně
Špatně
Členy nemůžeme sečíst/odečíst, nemáme ani co vytknout, musíme tedy použít algebraické vzorce.
Víme, že jsou tři typy – dva z nich mají 3 členy, třetí má pouze dva. My máme tři členy, vybíráme tedy vzorec podle znaménka u prostředního členu.
\((a+b)^2=a^2+2ab+b^2\).
Ze vzorce vidíme, že odmocníme první a třetí člen a dáme do závorky na druhou mocninu. Zkontrolujeme, jestli nám vychází prostřední člen. Kdyby nevycházel, příklad bychom neuměli nijak upravit. -
Otázka 10 / 10
10. Otázka
Rozlož na součin činitelů (postupné vytýkání):
\(5x^2-20y^2\)Správně
Špatně
Nemáme co upravit, můžeme ale vytknout. Vytkneme pouze číslo. V závorce nám zůstanou členy, které umíme ještě rozložit podle algebraického vzorce
\(a^2-b^2=(a-b)(a+b)\).
Rozložíme a nesmíme do výsledku zapomenout uvést i členy, které jsme vytkly v prvním kroku úpravy.
Zlomky - přijímačky
Procvičení vypočtů různých typů zlomků – 10 příkladů.
Zlomky - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení vypočtů různých typů zlomků – 10 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac {2}{3}\cdot \dfrac {1}{4}\cdot \left(-\dfrac {3}{2}\right)\)Správně
Špatně
\( +\: \cdot \:+\:⇒\: +\\
– \:\cdot\:\:+\:⇒ \:-\\
-\:\cdot\: \: -\:⇒ \:+\)
Zlomky násobíme tak, že násobíme čitatel s čitatelem a jmenovatel se jmenovatelem.
U násobení také můžeme krátit, do kříže nebo pod sebou. -
Otázka 2 / 10
2. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( 2+\sqrt {\dfrac {81}{121}}\)Správně
Špatně
Přednost má odmocnina. Odmocníme zlomek.
Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Dopočítáme a případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 3 / 10
3. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac {3}{5}^{2}-\dfrac {3}{5^{2}}+{\left(-\dfrac {3}{5}\right)^{2}}\)Správně
Špatně
Přednost má mocnina. Umocníme – pozor: zápor na druhou mocninu je ve výsledku klad.
Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Dopočítáme a případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 4 / 10
4. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\(\dfrac{\dfrac {7}{10}-\dfrac {2}{5}:\dfrac {2}{10}}{10\cdot \dfrac {3}{10}}\)Správně
Špatně
Máme složený zlomek. Je dobré nejdříve spočítat výsledek čitatele a potom jmenovatele. Můžete přímo do zlomku anebo bokem.
V čitateli má přednost dělení – zlomky neumíme dělit, převracíme na násobení. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Ve jmenovateli máme násobení, zkrátíme a vynásobíme čitatel s čitatelem a jmenovatel se jmenovatelem.
Máme výsledky složeného zlomku. Víme, že zlomková čára značí dělení. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 5 / 10
5. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( 0,16:\dfrac {2}{5}-\dfrac {3}{7}\cdot 1,05\)Správně
Špatně
Přednost má násobení a dělení, pak teprve sčítání/odčítání. Desetinné číslo převedeme na zlomek. Zlomky dělit neumíme, převracíme na násobení. Násobíme čitatele čitatelem a jmenovatele jmenovatelem. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar.
-
Otázka 6 / 10
6. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\(0,6-\dfrac {3}{5}\cdot\dfrac {8}{2}+1,9\)Správně
Špatně
Přednost má násobení, pak teprve sčítání/odčítání. Desetinné číslo převedeme na zlomek. Násobíme čitatele čitatelem a jmenovatele jmenovatelem. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar.
-
Otázka 7 / 10
7. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac{4\cdot \dfrac {2}{3}-3\dfrac {1}{3}}{1\dfrac {1}{2}\cdot 2\dfrac {2}{3}}\)Správně
Špatně
Máme složený zlomek. Je dobré nejdříve spočítat výsledek čitatele a potom jmenovatele. Můžete přímo do zlomku anebo bokem.
V čitateli má přednost násobení a smíšený zlomek si převedeme na základní tvar. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Ve jmenovateli máme násobení, zkrátíme a vynásobíme čitatel s čitatelem a jmenovatel se jmenovatelem.
Máme výsledky složeného zlomku. Víme, že zlomková čára značí dělení. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 8 / 10
8. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac{\left (\dfrac {1}{8}-\dfrac {1}{4}\right):\left(-\dfrac{5}{16}\right)}{0,7\cdot \dfrac {2}{7}- \left(-\dfrac {2}{5}\right)}\)Správně
Špatně
Máme složený zlomek. Je dobré nejdříve spočítat výsledek čitatele a potom jmenovatele. Můžete přímo do zlomku anebo bokem.
V čitateli má přednost závorka, potom dělení. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Zlomky dělit neumíme, převracíme na násobení. Ve jmenovateli převedeme desetinné číslo na zlomek, zkrátíme a vynásobíme čitatel s čitatelem a jmenovatel se jmenovatelem. Potom zase sčítáme/odčítáme.
Máme výsledky složeného zlomku. Víme, že zlomková čára značí dělení. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 9 / 10
9. Otázka
Vypočítej a výsledek zapiš smíšeným číslem:
\( \dfrac{\sqrt{\dfrac {4}{9}}:\sqrt{\dfrac {1}{36}}+\left(-\dfrac {1}{3}\right)^{2}\cdot 2\dfrac {2}{5}}{-0,3^{2}: \dfrac {3}{10}}\)Správně
Špatně
Máme složený zlomek. Je dobré nejdříve spočítat výsledek čitatele a potom jmenovatele. Můžete přímo do zlomku anebo bokem.
V čitateli i jmenovateli mají přednost mocniny a odmocniny. Dále násobení a dělení. Nakonec sčítání/odčítání. Zlomky dělit neumíme, převracíme na násobení. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Smíšené číslo převedeme na základní tvar. Ve jmenovateli převedeme desetinné číslo na zlomek.
Máme výsledky složeného zlomku. Víme, že zlomková čára značí dělení. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar. -
Otázka 10 / 10
10. Otázka
Vypočítej a výsledek zapiš v základním tvaru:
\( \dfrac{22:2,2-\left(-\dfrac {3}{2}\right)^2+\left(\sqrt{64}:1,6+3\dfrac {1}{2}\right)}{\left((\sqrt {9})^2-4:\dfrac {1}{4}\right)+15\cdot0,5^2}\)Správně
Špatně
Máme složený zlomek. Je dobré nejdříve spočítat výsledek čitatele a potom jmenovatele. Můžete přímo do zlomku anebo bokem.
V čitateli i jmenovateli mají přednost mocniny a odmocniny. Dále násobení a dělení. Nakonec sčítání/odčítání. Zlomky dělit neumíme, převracíme na násobení. Zlomky sčítáme/odčítáme tak, že najdeme společný jmenovatel a potom upravíme čitatele. Smíšené číslo převedeme na základní tvar. Desetinná čísla na zlomky.
Máme výsledky složeného zlomku. Víme, že zlomková čára značí dělení. Čitatel podělíme jmenovatelem, převrátíme na násobení a spočítáme. Případně zkrátíme čitatele i jmenovatele stejným číslem, abychom dostali základní tvar.
Celá čísla - přijímačky
Procvičení celých čísel – 10 příkladů.
Celá čísla - přijímačky
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičení celých čísel – 10 příkladů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej:
\(9:(-3)-14:(-7)\)Správně
Špatně
\( +\: : \:+\:⇒\: +\\
– \: : \:+\:⇒ \:-\\
-\: : \: -\:⇒ \:+\)
Přednost má dělení/násobení před sčítáním/odčítáním. -
Otázka 2 / 10
2. Otázka
Vypočítej:
\(45-2\cdot 15:(5-3)\)Správně
Špatně
\( +\: : \:+\:⇒\: +\\
– \: : \:+\:⇒ \:-\\
-\: : \: -\:⇒ \:+\)
Nejdříve spočítáme závorku, dále dělení/násobení a nakonec sčítání/odčítání. -
Otázka 3 / 10
3. Otázka
Vypočítej:
\(30-(20-20\cdot 3)+150\)Správně
Špatně
\( +\: : \:+\:⇒\: +\\
– \: : \:+\:⇒ \:-\\
-\: : \: -\:⇒ \:+\)
Nejdříve spočítáme závorku, ve které má přednost dělení/násobení před sčítáním/odčítáním. Výsledky potom sečteme. -
Otázka 4 / 10
4. Otázka
Vypočítej:
\(5+3\cdot (-4)-(8+4:2)\)Správně
Špatně
\( +\: : \:+\:⇒\: +\\
– \: : \:+\:⇒ \:-\\
-\: : \: -\:⇒ \:+\)
Nejdříve spočítáme závorku, ve které má přednost dělení/násobení před sčítáním/odčítáním. Dále má přednost násobení před sčítáním/odčítáním. Výsledky potom sečteme. -
Otázka 5 / 10
5. Otázka
Vypočítej:
\((-7)^2-(2)^2+(-5)^2\)Správně
Špatně
\( a^2 = a^2\\
– a^2 = – a^2\\
(- a)^2 = + a^2\)
Přednost mají mocniny. Nejdříve tedy umocníme, potom teprve sčítáme/odčítáme. -
Otázka 6 / 10
6. Otázka
Vypočítej:
\(3\cdot (5-2\cdot 2)-4\cdot (2-3)\)Správně
Špatně
Přednost mají závorky, v nich nejdříve násobení. Výsledky závorek teprve poté upravujeme a sčítáme/odčítáme výsledek.
-
Otázka 7 / 10
7. Otázka
Vypočítej:
\([-(-3)^2+5-2\cdot 2+4\cdot 2^2]^2\)Správně
Špatně
\( a^2 = a^2\\
– a^2 = – a^2\\
(- a)^2 = + a^2\)
Přednost má závorka. V ní nejdříve umocníme, poté násobíme/dělíme a až nakonec sčítáme/odčítáme. Až dostaneme výsledek závorky, teprve umocníme závorku. -
Otázka 8 / 10
8. Otázka
Vypočítej:
\(10^2+2\cdot(7^2-2\cdot 7)+5^2\)Správně
Špatně
\( a^2 = a^2\\
– a^2 = – a^2\\
(- a)^2 = + a^2\)
Umocníme, spočítáme závorku, její hodnotu ponásobíme a nakonec jednotlivé výsledky sečteme/odečteme. -
Otázka 9 / 10
9. Otázka
Vypočítej:
\(\sqrt{(8-3)+4}+\sqrt{225}:\sqrt{9}\)Správně
Špatně
Přednost mají odmocniny. Abychom mohli odmocnit, musíme nejdřív spočítat hodnotu pod odmocninou – přednost má závorka, poté sčítání/odčítání. Dostaneme výslednou hodnotu pod odmocninou a teď teprve odmocníme.
Dále pokračujeme podle pravidel – přednost má dělení před sčítáním. -
Otázka 10 / 10
10. Otázka
Vypočítej:
\(\sqrt{121}\cdot5-4(\sqrt{49\cdot4}+9:3)\)Správně
Špatně
Spočítáme hodnotu závorky. Pod odmocninou je násobení, můžeme odmocninu rozdělit – POZOR u +/- to není možné.
\( \sqrt{a\cdot b}= \sqrt{a}\cdot \sqrt{b}\)
Spočítáme odmocniny, upravíme závorku a dopočítáme výsledek.
Exponenciální rovnice
Procvičíte si exponenciální rovnice
Exponenciální rovnice
Exponenciální rovnice
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičíte si exponenciální rovnice – 20 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Vyřeš rovnici
\(3^{5m-8}=9^{m-3}\)Správně
Špatně
Pravou stranu rovnice převedeme na základ 3. Exponenty mezi sebou vynásobíme. Základy odstraníme a pracujeme pouze s exponenty. Dostali jsme lineární rovnici. Vyřešíme, případně si výsledek ověříme zkouškou.
-
Otázka 2 / 20
2. Otázka
Vyřeš rovnici
\(2^{x-4}=(\sqrt{2})^{2-3x}\)Správně
Špatně
Na pravé straně převede odmocninu na mocninu, tj. na 1/2. Exponenty mezi sebou vynásobíme, základy jsou na obou stranách stejné, dále pracujeme jen s exponenty. Vypočítáme kořen lineární rovnice a máme řešení.
-
Otázka 3 / 20
3. Otázka
Vyřeš rovnici
\(25\cdot 5^{x}\cdot\dfrac{1}{5^3} =1\)Správně
Špatně
Zlomek na levé straně umíme dát na základ 5 a pokud převádíme číslo z čitatele do jmenovatele a naopak, exponentům se mění znaménka. Levou i pravou stranu dáme na stejný základ, při násobení se exponenty sečtou, při dělení odečtou. Na pravé straně máme 1. Víme, že cokoliv na nultou je vždy 1. Odstraníme základy a dostaneme se k výsledku.
-
Otázka 4 / 20
4. Otázka
Vyřeš rovnici
\((5^{x})^3\cdot 0,2 =\dfrac{1}{25}\)Správně
Špatně
Při umocňování mocniny se základ opíše, exponenty se mezi sebou vynásobí. Desetinné číslo umíme převést na zlomek, 2/10, a ten umíme zkrátit. Zlomek na pravé straně umíme dát na základ 5 a pokud převádíme číslo z čitatele do jmenovatele a naopak, exponentům se mění znaménka. Levou i pravou stranu dáme na stejný základ, při násobení se exponenty sečtou, při dělení odečtou. Odstraníme základy a dostaneme se k výsledku.
-
Otázka 5 / 20
5. Otázka
Vyřeš rovnici
\(2^{2x^2-3x-1}=16\)Správně
Špatně
Pravou stranu upravíme na základ 2. Odstraníme základy a spočítáme kvadratickou rovnici. Zkontrolujeme, jestli oba kořeny vyhovují zadání.
-
Otázka 6 / 20
6. Otázka
Vyřeš rovnici
\(\sqrt{2^x}\cdot \sqrt{3^x}=36\)Správně
Špatně
Rovnici umocníme, tím odstraníme odmocniny. Obě čísla vlevo máme na stejnou mocninu, můžeme tedy nejdříve vynásobit a poté umocnit: \(\sqrt{2^x}\cdot \sqrt{3^x}=(2\cdot3)^x\).
Upravíme tak, aby na obou stranách byly stejné základy a rovnici dopočítáme. -
Otázka 7 / 20
7. Otázka
Vyřeš rovnici
\(\dfrac{27}{8}\cdot \left( \dfrac{2}{3}\right)^x=\dfrac {4}{9}\cdot\dfrac {9}{4}^{x+2}\)Správně
Špatně
Číselné hodnoty ve zlomcích umíme rozložit tak, abychom dostali nějaký základ na něco. Když takto rozložíme čitatele i jmenovatele, zjistíme, že máme oba na stejnou mocninu. V tomto případě tedy můžeme dát celý zlomek na jednu mocninu. Zjistíme, že zlomky všechny zlomky jsou téměř shodné. Kde nejsou, provedeme přetočení čitatele se jmenovatelem a exponent bude na zápornou mocninu. Už nám zbývá jen dát členy vlevo i vpravo na stejné základy, odstranit základy a spočítat rovnici, která vznikne s exponentů.
-
Otázka 8 / 20
8. Otázka
Vypočítej
\(0,25^{2-x}=\dfrac{256}{2^{x+3}}\)Správně
Špatně
Desetinné číslo převedeme na zlomek, ten umíme ještě zkrátit. Číslo v čitateli umíme rozložit na základ a exponent, jmenovatele můžeme převést k čitateli pomocí záporného exponentu. Vidíme, že základy ještě umíme upravit tak, aby byly stejné. Upravíme jejich exponenty. Získáme jeden základ vlevo, druhý stejný vpravo. Odstraníme základy, vypočítáme rovnici z exponentů a máme řešení.
-
Otázka 9 / 20
9. Otázka
Vypočítej
\(2^{(x-1)^2}\cdot \left(\dfrac{1}{2}\right)^38=\dfrac{1}{4}\)Správně
Špatně
V prvním exponentu použijeme na výpočet algebraický vzorec. Číslo v čitateli prvního a druhého zlomku umíme převést do čitateli pomocí záporného exponentu. Vidíme, že základy ještě umíme upravit tak, aby byly stejné. Upravíme jejich exponenty. Získáme jeden základ vlevo, druhý stejný vpravo. Odstraníme základy a vidíme, že nám vyšla kvadratická rovnice. Vypočítáme kořeny a ověříme, jestli oba vyhovují zadání.
-
Otázka 10 / 20
10. Otázka
Vypočítej
\(\left(\dfrac{3}{4}\right)^{x+2}\cdot \left(\dfrac{16}{9}\right)^{2x-3}=\dfrac{8}{27}\)Správně
Špatně
Čísla ve zlomcích umíme rozložit na základ a vhodný exponent. Druhý zlomek umíme přetočit pomocí záporného exponentu. Dostaneme stejné základy. Upravíme, abychom měli jeden základ vlevo, druhý stejný vpravo. Odstraníme základy a vypočítáme rovnici.
-
Otázka 11 / 20
11. Otázka
Vyřeš rovnici
\(3^{x+2}-3^{x+1}=162\)Správně
Špatně
V exponentech máme sčítání, umíme tedy základ rozdělit na více členů s různými exponenty. Základ s neznámou můžeme vytknout, vypočítáme hodnotu závorky, vydělíme a upravíme na stejný základ vlevo i vpravo. Dopočítáme a máme výsledek.
-
Otázka 12 / 20
12. Otázka
Vyřeš rovnici
\(3^{2x+3}+9^{x+1}+27^{\frac{2x}{3}}=999\)Správně
Špatně
V exponentech máme sčítání, umíme tedy základ rozdělit na více členů s různými exponenty. Potřebujeme mít stejné základy. Základ s neznámou můžeme vytknout, vypočítáme hodnotu závorky, vydělíme a upravíme na stejný základ vlevo i vpravo. Dopočítáme a máme výsledek.
-
Otázka 13 / 20
13. Otázka
Vyřeš rovnici
\(5\cdot \left(\dfrac{1}{5}\right)^{x+2}+10\cdot\left(\dfrac{1}{5}\right)^{x+1}=0,44\)Správně
Špatně
Závorky máme na exponent, který můžeme rozdělit. Desetinné číslo upravíme na zlomek. Vytkneme základ na „x“tou mocninu, spočítáme hodnotu závorky, rovnici poté závorkou vydělíme a dostaneme stejné základy vlevo i vpravo. Odstraníme a získáme výsledek.
-
Otázka 14 / 20
14. Otázka
Vyřeš rovnici
\(\dfrac{1}{6^{-3x-1}-6^{-3x-2}+6^{-3x}}=\dfrac{1}{246}\)Správně
Špatně
Ve jmenovateli máme základy na různé exponenty, které ale umíme rozdělit. Když je rozdělíme, vidíme, že můžeme vytknout. Jmenovatele umíme převést na čitatele, ale nesmíme zapomenout, že exponent bude záporný. Když máme násobení, tak každý člen má svůj exponent. Rovnici vydělíme tak, abychom na jedné straně měli základ s exponentem „x“ a na druhé straně číslo. Zjistíme, jestli číslo umíme dostat na požadovaný základ a dopočítáme.
-
Otázka 15 / 20
15. Otázka
Vyřeš rovnici
\(2^{x+5}-2^{x+3}+2^x=5^{x+1}-5^x\)Správně
Špatně
U jednotlivých základů rozdělíme exponenty, na každé straně rovnice vytkneme základ s neznámou. Potřebujeme mít neznámé na jedné straně a čísla na druhé. Víme, že pokud je čitatetel zlomku i jmenovatel na stejnou mocninu, můžeme dát celý zlomek na danou mocninu. Na pravé straně upravíme zlomek tak, abychom dostali stejný/podobný základ jako straně levé. Pokud máme stejné základy, porovnáme exponenty a máme výsledek.
-
Otázka 16 / 20
16. Otázka
Vyřeš rovnici
\(3^{2x+1}-3\cdot3^{x+2}=3^{x}-9\)Správně
Špatně
U jednotlivých základů rozložíme exponenty. Jeden ze základů má dvojnásobný exponent, musíme použít substituci. Např. \(2^x = y\). Dosadíme, spočítáme diskriminat a kořeny. Výsledky vrátíme do substituce, dopočítáme a máme konečný výsledek rovnice.
-
Otázka 17 / 20
17. Otázka
Vyřeš rovnici
\(25^{2x}-3\cdot 5^{2x}=10\)Správně
Špatně
Rozložíme základy tak, abychom je dostaly stejné. Můžeme pracovat se základem 25 nebo 5. Obě varianty musí vyjít stejně. Využijeme substituci, např. \(2^{2x}=a\).
Vypočítáme kořeny kvadratické rovnice a vrátíme do substituce. Teprve poté dostaneme výsledek. -
Otázka 18 / 20
18. Otázka
Vyřeš rovnici
\(4^{x}+7\cdot 2^{x-2}=0,5\)Správně
Špatně
Rozložíme na stejné základy, případně rozhodíme exponenty. Desetinné číslo upravíme na zlomek. Z rovnice je dobré odstranit zlomky, aby se nám lépe počítalo. Využijeme substituci, např. \(3^{x}=y\).
Vypočítáme kořeny kvadratické rovnice a vrátíme do substituce. Teprve poté dostaneme výsledek. -
Otázka 19 / 20
19. Otázka
Vyřeš rovnici
\(5\cdot 4^{-x+2}=2\cdot 4^{4-x}-27\)Správně
Špatně
U základů rozdělíme exponenty. Není třeba je nijak zvlášť upravovat, můžeme potom rovnout použít substituci. Dostaneme jednoduchou lineární rovnici. Vypočítáme a dosadíme do substituce. Výsledek je potom řešením rovnice.
-
Otázka 20 / 20
20. Otázka
Vyřeš rovnici
\(\dfrac{1}{4}\cdot 2^{x}+\dfrac{1}{4}\cdot 4^{x}=5\)Správně
Špatně
V rovnici nejdříve odstraníme zlomky – celou rovnici vynásobíme. Upravíme na stejné základy, využijeme substituci a dostaneme kvadratickou rovnici. Vyřešíme kořeny, které dosadíme do substituce. Vyřešíme exponenciální rovnici a dostaneme řešení.
Operace s mnohočleny I.
Procvičíte si sčítání a odčítání mnohočlenů od lehčí až po ty náročnější.
Operace s mnohočleny I.
Závěrečný přehled
Zodpovězeno 0 z 28 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
Information
Procvičíte si sčítání a odčítání mnohočlenů od lehčíš až po ty náročnější. Dále si procvičíte, jak umíte mnohočleny mezi sebou násobit.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 28 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 28
1. Otázka
Vypočítej
\(9c^2-4c-4c^2+5c\)Správně
Špatně
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent. Neznámé sice stejné máme, ale exponenty jsou různé. Nemůžeme tedy sečíst vše dohromady.
Sečteme čísla u c a čísla u c na druhou mocninu.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 2 / 28
2. Otázka
Vypočítej
\(3h^3-2h^2+h-h^3-2h^2+h\)Správně
Špatně
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent. Neznámé sice stejné máme, ale exponenty jsou různé. Nemůžeme tedy sečíst vše dohromady.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 3 / 28
3. Otázka
Vypočítej
\((am+4b+7)-(4+am-m)\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na zmanémko mínus před závorkou – mění nám všechna znaménka v závorce.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 4 / 28
4. Otázka
Vypočítej
\(4x-(2x+y)+7y-(x-y)\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na zmanémko mínus před závorkou – mění nám všechna znaménka v závorce.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 5 / 28
5. Otázka
Vypočítej
\((-4a^2x+ax^2-3a^2x^2)+(-ax^2+2xa^2-x^2a^2)\)Správně
Špatně
Nejdříve odstraníme závorky.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent. Pozor, u součinu nezáleží na pořadí, proto ax = xa. Musíme akorát dávat pozor na exponenty.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 6 / 28
6. Otázka
Vypočítej
\((ab^2+ba^2)-(3-b^2a+ab)+(2a^2b-2ab+1)\)Správně
Špatně
Nejdříve odstraníme závorky.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent. Pozor, u součinu nezáleží na pořadí, proto např. ax = xa. Musíme akorát dávat pozor na exponenty.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 7 / 28
7. Otázka
Vypočítej
\((12m^2n+n-m)-2nm^2+n-(-m-2n)\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na mínus před závorkou.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent. Pozor, u součinu nezáleží na pořadí, proto ax = xa. Musíme akorát dávat pozor na exponenty.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 8 / 28
8. Otázka
Vypočítej
\(2a-[2a+b-(3a-2b)-(a-b)]\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na mínus před závorkou. Závorky odstraňuje od vnitřních po vnější, tj. nejdříve kulaté, potom hranatou.
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 9 / 28
9. Otázka
Vypočítej
\(1,7a^2-10b^2-\lbrace a^2-3b^2-[4,3a^2-(2a^2-7b^2)]\rbrace\)Správně
Špatně
Nejdříve odstraníme závorky. Pozor na mínus před závorkou. Závorky odstraňuje od vnitřních po vnější, tj. nejdříve kulaté, potom hranatou a nakonec množinovou (složenou).
Dáme dohromady členy, které mají stejnou neznánou a zároveň stejný exponent.
Můžete si např. při výpočtu stejné členy různě podrthnout, dát do barevných koleček, …. -
Otázka 10 / 28
10. Otázka
Vypočítej
\(6a-\lbrace-[2b+3a-(3b-a)-2a]+b\rbrace\)Správně
Špatně
Odstraníme závorky, pozor na mínus před závorkou. Nejdříve odstraníme kulaté, potom hranaté a nakonec množinové.
Členy se stejnou neznámou sečteme. -
Otázka 11 / 28
11. Otázka
Vypočítej
\(8m\cdot (-0,5m)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 12 / 28
12. Otázka
Vypočítej
\(-6t\cdot (-0,3tu)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 13 / 28
13. Otázka
Vypočítej
\(9a\cdot (-a) \cdot (-7a)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 14 / 28
14. Otázka
Vypočítej
\(2ab\cdot (-5bc) \cdot 3ac\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 15 / 28
15. Otázka
Vypočítej
\(-a^2\cdot 8ab \cdot (-2bc)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 16 / 28
16. Otázka
Vypočítej
\((7x-6)\cdot (-4x)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Roznásobíme závorku tak, že každý člen dvojčlenu vynásobíme jednočlenem. Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. -
Otázka 17 / 28
17. Otázka
Vypočítej
\(2+3a\cdot (4-a)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Roznásobíme závorku tak, že každý člen dvojčlenu vynásobíme jednočlenem. Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 18 / 28
18. Otázka
Vypočítej
\((7y-4)\cdot (-3y)-5y\cdot(1-2y)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Roznásobíme závorky tak, že každý člen dvojčlenu vynásobíme jednočlenem. Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 19 / 28
19. Otázka
Vypočítej
\([2x\cdot (6x^2-2xy+3)-4\cdot (x^3-x^2y)]\cdot (-2y)\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Roznásobíme nejdříve kulatou závorku tak, že každý člen trojčlenu/dvojčlenu vynásobíme jednočlenem. Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. Členy v hranaté závorce můžeme upravit a teprvé poté vynásobit jednočlenem. Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 20 / 28
20. Otázka
Vypočítej
\(-2a^2\cdot\lbrace 6ab\cdot [-ab+3(a^2b-3ab^2)]+2a^2b\rbrace\)Správně
Špatně
\(+ \:\cdot \: – \:⇒\: -\\
+\: \cdot \: +\: ⇒ \:+\\
– \:\cdot \:- \:⇒ \:+\\\)
Roznásobíme nejdříve kulatou závorku tak, že každý člen dvojčlenu vynásobíme číslem. Dále se zbavíme obdobným způsobem závorky hranaté.Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme. Nakonec teprve všechny členy množinové závorky vynásobíme jednočlenem. Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 21 / 28
21. Otázka
Vynásob mnohočleny
\((6ij-5i)\cdot(2ij+3j)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 22 / 28
22. Otázka
Vypočítej
\(-6c\cdot(4-c)(5c-3)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Je jedno, jestli nejdříve vynásobíme jednočlen dvojčlenem a pak teprve výsledek dalším dvojčlenem anebo můžeme nejdřív vynásobit dvojčleny a pak až vynásobit jednočlenem.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 23 / 28
23. Otázka
Vynásob mnohočleny
\((x-y)(x+z)(y-z)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Nejdříve vynásobíme dvě závorky mezi sebou, teprve poté výsledek vynásobíme zbývající závorkou.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 24 / 28
24. Otázka
Vypočítej
\((3x-5)\cdot[3x-5(3x-5)]\)Správně
Špatně
Musíme nejdříve upravovat závorky, jdeme od kulaté, potom teprve hranatou a nakonec násobíme mnohočleny.
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 25 / 28
25. Otázka
Vypočítej
\((5x-2y)(3x-4y+5)+(2x+5)(x-3)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 26 / 28
26. Otázka
Vypočítej
\((a^4-a^3b+a^2b^2-ab^3+b^4)(a+b)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 27 / 28
27. Otázka
Vypočítej
\((5m^2-3m^3+4m-1)(3-2m^2-6m)\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst. -
Otázka 28 / 28
28. Otázka
Vypočítej
\((c+1)\lbrace 2c(c-1)-(c+2)[(3c-2)(c+1)-(c^2-9)]\rbrace\)Správně
Špatně
Mnohočlen vynásobíme mnohočlenem tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého mnohočlenu, tj. zkráceně: násobíme každý s každým.
Vynásobíme čísla mezi sebou. Proměnné násobíme tak, že neznámou opíšeme a exponenty sečteme.
Řešíme nejdříve vnitřní závorky a postupně odstraňujeme další, tzn. nejdříve kulaté, potom hranatou a nakonec odstraníme množinovou.
Ještě zkontrolujeme, jestli se nějaké členy dají mezi sebou sečíst/odečíst.
Operace s mnohočleny II.
Procvičíte si dělení mnohočlenů. Dále si procvičíte určení hodnoty výrazu v případě, že za proměnou dosadíme zadanou hodnotu.
Operace s mnohočleny II.
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičíte si dělení mnohočlenů – jednočlen jednočlenem, mnohočlen jednočlenem a také mnohočlen děleno mnohočlenem. Dále si procvičíte určení hodnoty výrazu v případě, že za proměnou dosadíme zadanou hodnotu.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
Vypočítej
\(72xy^2:(-9y^2)\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Vydělíme čísla mezi sebou. Proměnné dělíme tak, že neznámou opíšeme a exponenty odečteme. -
Otázka 2 / 20
2. Otázka
Vypočítej
\(-60x^2y^2:12xy\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Vydělíme čísla mezi sebou. Proměnné dělíme tak, že neznámou opíšeme a exponenty odečteme. -
Otázka 3 / 20
3. Otázka
Vypočítej
\((24xy-16y):8y\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Pokud dělíme mnohočlen jednočlenem, vydělíme každý člen mnohočlenu jednočlenem zvlášť. Vydělíme čísla mezi sebou a proměnné dělíme tak, že neznámou opíšeme a exponenty odečteme. -
Otázka 4 / 20
4. Otázka
Vypočítej
\((-36a^3b+60a^2b^2-84a^3b^3):(-12a^2b)\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Mnohočlen vydělíme jednočlenem tak, že každý člen mnohočlenu vydělíme zvlášť. Při dělení nejdříve vydělíme čísla mezi sebou a neznámou dělíme tak, že základ opíšeme a exponenty odečteme. -
Otázka 5 / 20
5. Otázka
Vypočítej
\((34c^3-85c^2):(-17)c^2-(45c^2-10c):(-5c)\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Nejdříve odstraníme závorky. Dělíme mnohočlen jednočlenem tak, že každý člen mnohočlenu vydělíme zvlášť. Při dělení nejdříve vydělíme čísla mezi sebou a neznámou dělíme tak, že základ opíšeme a exponenty odečteme.
Zkontrolujeme, jestli se nějaké členy dají sečíst/odečíst. -
Otázka 6 / 20
6. Otázka
Vypočítej
\((12a^3b^2+30a^2b-54a):6a-(-48a^2b^3+12ab^3):12b^2\)Správně
Špatně
\(+ \: : \: – \:⇒\: -\\
+\: : \: +\: ⇒ \:+\\
– \: : \:- \:⇒ \:+\\\)
Odstraníme závorky. Mnohočlen vydělíme jednočlenem tak, že každý člen mnohočlenu vydělíme zvlášť. Při dělení nejdříve vydělíme čísla mezi sebou a neznámou dělíme tak, že základ opíšeme a exponenty odečteme.
Zkontrolujeme, jestli se některé členy dají sečíst/odečíst. -
Otázka 7 / 20
7. Otázka
Vypočítej
\((x^3-x^2-7x+3):(x-3)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit. -
Otázka 8 / 20
8. Otázka
Vypočítej
\((10+6a^3-9a-13a^2):(2a-5)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit. -
Otázka 9 / 20
9. Otázka
Vypočítej
\((3x^3+x^3+2x^2-x+1):(x^2+x+1)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit. -
Otázka 10 / 20
10. Otázka
Vypočítej
\((27x^7+2x^5+10x^10-15x^9+3x^3-5x+5x^2-3x^6):(5-3x^2+2x^3)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit. -
Otázka 11 / 20
11. Otázka
Vypočítej
\((x^7+2):(x+1)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit.
Pokud nám vyjde zlomek, nesmíme ho zapomenout zapsat k výsledku. -
Otázka 12 / 20
12. Otázka
Vypočítej
\((2a^4-5a^3+16a^2-3a+2):(2a^2-a)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit.
Pokud nám vyjde zlomek, nesmíme ho zapomenout zapsat k výsledku. -
Otázka 13 / 20
13. Otázka
Vypočítej
\((12c-16+9c^2+c^3):(0,5c^2-3c-4)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit.
Pokud nám vyjde zlomek, nesmíme ho zapomenout zapsat k výsledku. -
Otázka 14 / 20
14. Otázka
Vypočítej
\((b^5-3b^2+5):(b^2-1)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit.
Pokud nám vyjde zlomek, nesmíme ho zapomenout zapsat k výsledku. -
Otázka 15 / 20
15. Otázka
Vypočítej
\((-2u^7-4u^5+6u^3+4+7u^6-12u^4+3u^2):(-u^3+u-2u^4+2u^2)\)Správně
Špatně
Při dělení mnohočlenu mnohočlenem musíme nejdříve zkontrolovat, jestli jsou členy dělence i dělitele uspořádány, např. od nejvyššího exponentu po nejnižší.
Samotné dělení potom probíhá stejně jako klasické dělení s „ocáskem“.
Vydělíme první člen mnohočlenu prvním členem druhého mnohočlenu, napíšeme výsledek a výsledkem násobíme všechny členy dělitele.
Postup opakujeme, dokud nedostaneme zbytek 0 nebo takový člen, který již neumíme dělit.
Pokud nám vyjde zlomek, nesmíme ho zapomenout zapsat k výsledku. -
Otázka 16 / 20
16. Otázka
Vypočítej hodnotu čtyřčlenu pro x = 0,5, y = – 0,2
\(3x^2-2xy + 5y^2-6\)
Správně
Špatně
Abychom určili hodnotu výrazu, dosadíme za neznámou x zadané číslo a to samé s neznámou y. Podle pravidel pro počítání upravíme a dostaneme výslednou hodnotu.
-
Otázka 17 / 20
17. Otázka
Zjednoduš výraz a správnost výsledku ověř výpočtem hodnoty původního a výsledného výrazu pro \(a=-1,\: b=3\)
\((8a^2-7a-3b-6b^2)-(9a^2-5a-3b+4b^2)\)
- Výsledný výraz je (-1, -)a2 (-2)a (+0, -0, 0)b (-10)b2. Hodnota původního i výsledného výrazu je (-89).
Správně
Špatně
Nejdříve upravíme mnohočlen – odstraníme závorky, sečteme/odečteme členy, které mají stejnou neznámou a zároveň stejný exponent.
Abychom určili hodnotu původního a výsledného výrazu, dosadíme za neznámou a zadané číslo a to samé s neznámou b. Dosazujeme nejdříve do zadání a poté do námi upraveného výsledku. Pokud se nám hodnoty rovnají, máme výpočet mnohočlenu správně.Nápověda
Čísla k proměnným (neznámým) zapisujte i se znaménky.
-
Otázka 18 / 20
18. Otázka
Zjednoduš a potom vypočítej hodnotu výrazu pro u = \(\dfrac{1}{2}\)
\((2u^2+3u-1)-(3u^2-2u+9)\)
Správně
Špatně
Abychom uměli spočítat hodnotu mnohočlenu, musíme nejdříve upravit daný výraz.
Odstraníme závorky, pozor na mínus před závorkou. Členy se stejnou neznámou a stejným exponentem sečteme/odečteme a máme výsledek.
Do výsledku dosadíme zadanou hodnotu a spočítáme hodnotu výrazu. -
Otázka 19 / 20
19. Otázka
Zjednoduš výraz a správnost výsledku ověř výpočtem hodnoty původního a\(\nobreakspace\)výsledného výrazu pro s = \(\dfrac{1}{2}\), t = \(-\dfrac{1}{3}\)
\(-5s+8t-[(7t-3s+8ts)-(4s-5ts+6t)]\)
- Výsledný výraz je (2, +2)s (+7)t (-13)ts. Hodnota původního i výsledného výrazu je (5/6, +5/6).
Správně
Špatně
Máme zjednodušit výraz – odstraníme nejdříve závorky. Začneme od vnitřních po vnější. Pozor na znaménka mínus před závorkami.
Správnost výpočtu zjistíme tak, že zadané hodnoty dosadíme do původního výrazu a poté i do výsledného výrazu. Pokud se nám spočítané hodnoty rovnají, máme výsledný výraz dobře spočítaný.Nápověda
Čísla k proměnným zapisujte i se znaménky.
V případě, že hodnota výrazu vyjde ve zlomku, zapište zlomek lomítkem, např. 1/3; 8/5 -
Otázka 20 / 20
20. Otázka
Zjednoduš výraz a správnost výsledku ověř výpočtem hodnoty původního a výsledného výrazu pro b = – 1, c = 2
\(bc(11c-7b)-[(b-2c)\cdot(b^2-5bc+c^2)+c^3]\)
- Výsledný výraz je (1, +1)c3 (0, +0)c2b (0, +0)cb2 (-1)b3 Hodnota původního i výsledného výrazu je (9, +9).
Správně
Špatně
Máme zjednodušit výraz – odstraníme nejdříve závorky. Začneme od vnitřních po vnější. Pozor na znaménka mínus před závorkami. Roznásobíme mnohočlen mnohočlenem. Sečteme/odečteme členy se stejnou proměnnou a stejným exponentem.
Správnost výpočtu zjistíme tak, že zadané hodnoty dosadíme do původního výrazu a poté i do výsledného výrazu. Pokud se nám spočítané hodnoty rovnají, máme výsledný výraz dobře spočítaný.Nápověda
Čísla k proměnným (neznámým) zapisujte i se znaménky.
Desetinná čísla - Procvičování
Procvičíte si počítání s desetinnými čísly – převod ze zlomku na desetinné a naopak, sčítání/odčítání, násobení/dělení, umocnění/odmocnění
Desetinná čísla - Procvičování
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Procvičíte si počítání s desetinnými čísly – převod ze zlomku na desetinné a naopak, sčítání/odčítání, násobení/dělení, umocnění/odmocnění.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočítej
\(4\cdot 0,2^2\)Správně
Špatně
Přednost má umocnění. Při umocňování desetinného čísla se počet desetinných míst ve výsledku násobí. Poté už jen vynásobíme číslem a dáme opět pozor na desetinnou čárku.
-
Otázka 2 / 10
2. Otázka
Vypočítej
\((4,5-3,45):(3,5-3)\)Správně
Špatně
Nejdříve spočítáme výsledky závorky, poté tyto mezi sebou vydělíme. Desetinným číslem neumíme dělit, musíme nejdřív upravit tak, abychom v děliteli odstranili desetinné číslo.
-
Otázka 3 / 10
3. Otázka
Vypočítej
\((-7,9):79+0,5^2:0,25-\sqrt{0,64}\cdot (-0,3)^2\)Správně
Špatně
Přednost má umocnění/odmocnění před násobením a dělením. Některé mezivýpočty můžeme ale dělat dohromady. Při dělení dáváme pozor, abychom nedělili desetinným číslem, při odmocnění, umocnění a násobení si hlídejte výsledný počet desetinných míst. Poté už jen mezivýpočty sečteme a odečteme a dostaneme výsledek.
-
Otázka 4 / 10
4. Otázka
Vypočítej
\(\dfrac{\dfrac{1}{5}\cdot 2^2-\sqrt{0,0121}:2,2}{(0,4+0,5)^2\cdot \sqrt{1,96}}\)Výsledek zaokrouhli na 4 desetinná místa.
Správně
Špatně
V čitateli zlomek převedeme na desetinné číslo, umocníme, odmocníme, podělíme a poté teprve odčítáme. Ve jmenovateli spočítáme nejdříve závorku, tu umocníme a vynásobíme odmocněným číslem.
Zlomková čára nám značí dělení, vydělíme tedy čitatele jmenovatelem a dostaneme výsledek. -
Otázka 5 / 10
5. Otázka
Vypočítej
\((2\cdot 4,02+0,12):(3\cdot0,9 – 0,3)\)Správně
Špatně
Přednost mají závorky. V závorkách nejdříve spočítáme násobení, potom teprve přičteme/odečteme. Výsledky závorek mezi sebou vydělíme a získáme konečný výsledek.
-
Otázka 6 / 10
6. Otázka
Vypočítej
\(1,2\cdot 0,5-0,16:\dfrac{2}{25}+0,3\)Správně
Špatně
Přednost má dělení/násobení před sčítáním a odčítáním. Zlomek si převedeme na desetinné číslo. Dáváme pozor na desetinné čárky při násobení a víme, že desetinným číslem neumíme dělit. Upravíme se tedy číslo tak, abychom měli dělitel bez desetinné čárky.
-
Otázka 7 / 10
7. Otázka
Vypočítej
\(-(0,02-0,1)-[-1-0,1-0,01-(1+0,1+0,01)]\)Správně
Špatně
Přednost mají závorky, postupujeme od vnitřních po vnější. Vypočítáme hodnoty v kulatých závorkách, případně upravíme znaménko a spočítáme hodnotu v hranaté závorce. Výsledky dáme dohromady a máme konečný výsledek.
-
Otázka 8 / 10
8. Otázka
Vypočítej
\(-0,06-0,1^2+(0,04^2+0,01)-\sqrt{0,09}\)Správně
Špatně
Přednost mají mocniny a odmocniny, potom teprve sčítání/odčítání. Při umocňování se počet desetinných míst násobí, při odmocňování se naopak půlí.
-
Otázka 9 / 10
9. Otázka
Vypočítej
\(-(-0,4)^2+0,14-(0,5^2-0,6^2)+\sqrt{9+16}\)Správně
Špatně
Přednost mají mocniny a odmocniny před sčítáním a odčítáním. Pokud je pod odmocninou +/-, musíme nejdřív upravit a pak teprve odmocníme. Dáváme pozor na desetinná místa, která při umocnění násobíme a při odmocňování půlíme.
-
Otázka 10 / 10
10. Otázka
Vypočítej
\(1,4^2+\sqrt{0,04}-\left(\dfrac{3}{10}\right)^2-\sqrt{\dfrac{21}{100}+\dfrac{60}{100}}\)Správně
Špatně
Zlomek převedeme na desetinné číslo, členy umocníme nebo odmocníme. Pod odmocninou máme sčítání, které má přednost. Poté teprve odmocníme. Jednotlivé mezivýsledky sečteme/odečteme a dostaneme konečný výsledek. Při umocňování a odmocňování dáme pozor na počet desetinných míst.
Integrály - tabulkové
Deset příkladů na procvičení základních tabulkových integrálů.
Integrály - tabulkové
Integrály – tabulkové
Závěrečný přehled
Zodpovězeno 0 z 10 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Deset příkladů na procvičení základních tabulkových integrálů.
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 10 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
Rubriky
- Žádná rubrika 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 10
1. Otázka
Vypočtěte integrál:
\(\displaystyle\int cos(x)dx\)Správně
Špatně
Jedná se o základní tabulkový integrál.
-
Otázka 2 / 10
2. Otázka
Vypočtěte integrál:
\(\displaystyle\int \dfrac{tg(x)}{sin(2x)}dx\)Správně
Špatně
Použijte goniometrické vzorce a upravte funkci \(tg(x)=\frac{sinx}{cosc}\) a funkci \(sin2x=2sinxcosx\).
-
Otázka 3 / 10
3. Otázka
Vypočtěte integrály:
\(\displaystyle\int \dfrac{x+1}{\sqrt{x}}dx\)Správně
Špatně
Upravte na součet dvou integrálů.
-
Otázka 4 / 10
4. Otázka
Vypočtěte integrál:
\(\displaystyle\int \dfrac{6}{x^3}dx\)Správně
Špatně
Vytkněte konstantu před integrál a ze jmenovatele převeďte \(x^3\) do čitatele zlomku.
-
Otázka 5 / 10
5. Otázka
Vypočtěte integrál:
\(\displaystyle\int \dfrac{5}{x^2+4}dx\)Správně
Špatně
Vytkněte konstantu před integrál a ve jmenovateli upravte členy tak, aby oba byly „na druhou“.
-
Otázka 6 / 10
6. Otázka
Vypočtěte integrál:
\(\displaystyle\int cotg^2x dx\)Správně
Špatně
Upravte pomocí goniometrických vzorců. Použijte vztahy \(cotg(x)=\dfrac{cosx}{sinx}\) a také \(sin^2x+cos^2x=1\)
-
Otázka 7 / 10
7. Otázka
Vypočtěte integrál:
\(\displaystyle\int \dfrac{e^x-e^{2x}+1}{e^x}dx\)Správně
Špatně
Zlomek rozdělte na tři zlomky a ty potom každý zvlášť integrujte.
-
Otázka 8 / 10
8. Otázka
Vypočtěte integrál:
\(\displaystyle\int (5x^4-x^3+10x)dx\)Správně
Špatně
Použijte vzorec pro integrování součtu funkcí.
-
Otázka 9 / 10
9. Otázka
Vypočtěte integrál:
\(\displaystyle\int (2x-6)^3 dx\)Správně
Špatně
Použijte vzoreček „na třetí“ a jednotlivé členy integrujte.
-
Otázka 10 / 10
10. Otázka
Vypočtěte integrál:
\(\displaystyle\int (8^x+2^xln(2)) dx\)Správně
Špatně
Integrál rozdělte na dva integrály a nezapomeňte, že \(ln(2)\) je v tomto případě konstanta, protože neobsahuje proměnnou \(x\).
Matice I.
Procvičíte si sčítání/odčítání matic, násobení matice konstantou, výpočty rovnic, ve kterých se objevují matice – 8 příkladů
Matice I.
Závěrečný přehled
Zodpovězeno 0 z 8 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Information
Procvičíte si sčítání/odčítání matic, násobení matice konstantou, výpočty rovnic, ve kterých se objevují matice – 8 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 8 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 8
1. Otázka
Vypočítej
\(A-B+C\), jsou-li matice\[
A= \begin{pmatrix}
1 & 3 & 2 \\
7 & 2 & 0 \\
1 & 0& 1
\end{pmatrix} \qquad B=
\begin{pmatrix}
3 & -1 & 1 \\
4 & -4 & 5 \\
8&-2 & 4
\end{pmatrix}\qquad C=
\begin{pmatrix}
2 & -2 &0 \\
-3 & 1 &2 \\
4&3& -3
\end{pmatrix}
\]Správně
Špatně
Matice sčítáme/odčítáme po prvcích. Můžeme nejdříve spočítat hodnotu matice A-B, poté k výsledku přičíst matici C. Také můžeme spočítat rozdíl a součet matic naráz.
Vezmeme první člen matice A, odečteme první člen matice B a přičteme první člen matice C. Dostáváme první člen výsledné matice. Stejně postupujeme pro další členy.
Dáváme pozor na znaménko mínus před maticí – funguje to stejně jako mínus před závorkou. -
Otázka 2 / 8
2. Otázka
Vypočítej hodnotu matice X, pro kterou platí
\(X=2\cdot(A-C)+B\), jsou-li matice\[
A= \begin{pmatrix}
3 & 0 & 3 \\
5 & 2 & 3
\end{pmatrix} \qquad B=
\begin{pmatrix}
1 & 2 & 4 \\
-2 & 0 & -3
\end{pmatrix}\qquad C=
\begin{pmatrix}
-1 & 2 &1 \\
-3 & 0 &5
\end{pmatrix}
\]Správně
Špatně
Nejdříve spočítáme rozdíl matic A a C, vynásobíme dvěma. Teprve k tomuto výsledku přičteme matici B.
Matice sčítáme/odčítáme po prvcích. Násobení matice konstantou znamená, že každý člen matice vynásobíme daným číslem. -
Otázka 3 / 8
3. Otázka
Vypočítej
\(3\cdot(A-B)\), jsou-li matice\[
A= \begin{pmatrix}
\dfrac{1}{2} & \dfrac{7}{4} & 1 \\
2 & -\dfrac{1}{2} & \dfrac{8}{3}\\
4&2&\dfrac{1}{3}
\end{pmatrix} \qquad B=
\begin{pmatrix}
2 & 0 & \dfrac{2}{3} \\
-\dfrac{3}{4} & -\dfrac{1}{2} & \dfrac{1}{2}\\
-1&0&-\dfrac{2}{3}
\end{pmatrix}
\]Správně
Špatně
Nejdříve spočítáme rozdíl matic, teprve poté vynásobíme.
Matice sčítáme/odčítáme po prvcích. Číslem potom vynásobíme každý člen matice. -
Otázka 4 / 8
4. Otázka
Z dané rovnice vypočítej hodnotu matice X
\(3A-2X=4B-3A\), jsou-li matice\[
A= \begin{pmatrix}
1 & 2 &-3&4 \\
0 &1&-2&3\\
0&0&1&4\\
-1&-2&0&1
\end{pmatrix} \qquad B=
\begin{pmatrix}
3 & 2& 1&0 \\
-2& -1 & 0&2 \\
6&0&-2&5\\
1&0&1&0
\end{pmatrix}
\]Správně
Špatně
Nejdříve upravíme rovnici. Pracujeme stejně, jako bychom měli lineární rovnici, tzn. neznámou na jednu stranu, zbytek na druhou. Potřebujeme ve výsledku jednu kladnou neznámou.
Jakmile si takto vyjádříme výpočet matice X, můžeme počítat. Přednost má násobení konstantou, potom teprve sčítání/odčítání.
Konstantou násobíme každý člen matice, matice sčítáme/odčítáme po prvcích. -
Otázka 5 / 8
5. Otázka
Z dané rovnice vypočítej hodnotu matice X
\(4A+3X=4(X-B)+2C\), jsou-li matice\[
A= \begin{pmatrix}
3 & 1 \\
-6 &5
\end{pmatrix} \qquad B=
\begin{pmatrix}
0 & 3 \\
-2&4
\end{pmatrix}\qquad C=
\begin{pmatrix}
-1 & 2 \\
3&-4
\end{pmatrix}
\]Správně
Špatně
Rovnici upravíme tak, abychom na jedné straně měli neznámou a na druhé čísla. Při přechodu přes znaménko rovnosti, měníme plus na mínus a opačně.
Jakmile máme vyjádřenou jednu kladnou neznámou, dosadíme matice a počítáme. Při násobení konstantou násobíme každý člen matice. Matice sčítáme/odčítáme po prvcích. -
Otázka 6 / 8
6. Otázka
Z dané rovnice vypočítej hodnotu matice X
\(2(A-X)+B=3(A-B)+3(X+C)\), jsou-li matice\[
A= \begin{pmatrix}
\dfrac{1}{2} & 2&-3 \\
-\dfrac{5}{2} &-5&0
\end{pmatrix} \qquad B=
\begin{pmatrix}
\dfrac{25}{2} & \dfrac{5}{3}&5 \\
0&\dfrac{20}{6}&\dfrac{15}{2}
\end{pmatrix}\qquad C=
\begin{pmatrix}
1 & -\dfrac{1}{2}&0 \\
3&-\dfrac{2}{3}&-\dfrac{3}{2}
\end{pmatrix}
\]Správně
Špatně
Rovnici upravíme tak, abychom na jedné straně měli neznámou a na druhé čísla. Při přechodu přes znaménko rovnosti, měníme plus na mínus a opačně.
Jakmile máme vyjádřenou jednu kladnou neznámou, dosadíme matice a počítáme. Při násobení konstantou násobíme každý člen matice. Matice sčítáme/odčítáme po prvcích. -
Otázka 7 / 8
7. Otázka
Najděte matici X, pro kterou platí
\[
3\cdot\left[X+2\cdot \begin{pmatrix}
1 & 3&1\\
3&-1&1\\
1&1&-3
\end{pmatrix}\right]=
4\cdot \left[X-\begin{pmatrix}
1 & -2&-3\\
-3&2&1\\
2&1&-3\end{pmatrix}\right] \]Správně
Špatně
Rovnici upravíme tak, abychom na jedné straně měli neznámou a na druhé čísla. Při přechodu přes znaménko rovnosti, měníme plus na mínus a opačně.
Zároveň provádíme výpočty s maticemi. Při násobení konstantou násobíme každý člen matice. Matice sčítáme/odčítáme po prvcích. -
Otázka 8 / 8
8. Otázka
Najděte matici X, pro kterou platí
\[
X-3\cdot\begin{pmatrix}
2 & 4&-1\\
3&0&-2\\
-1&1&-1
\end{pmatrix}=
2\cdot \left\{ X-4\cdot\left[\begin{pmatrix}
3 & 1&0\\
2&0&-1\\
1&3&0\end{pmatrix}-\begin{pmatrix}
-1 & 0&1\\
2&1&-3\\
4&-2&6\end{pmatrix}\right]\right \}
\]Správně
Špatně
Rovnici upravíme tak, abychom na jedné straně měli neznámou a na druhé čísla. Při přechodu přes znaménko rovnosti, měníme plus na mínus a opačně.
Zároveň provádíme početní operace s maticemi. Dáváme pozor na závorky. Při násobení konstantou násobíme každý člen matice. Matice sčítáme/odčítáme po prvcích.
Matice II.
Procvičení transponované matice a násobení matic – 11 příkladů
Matice II.
Závěrečný přehled
Zodpovězeno 0 z 11 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Information
Procvičení transponované matice a násobení matic – 11 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 11 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 11
1. Otázka
Vypočítej
\(A\cdot B^T\), jsou-li matice
\[
A=\begin{pmatrix}
8&0&11&3\\
7&6&0&10\\
2&9&4&1
\end{pmatrix}\qquad B=\begin{pmatrix}
2&10&7&5\\
10&3&7&12
\end{pmatrix}
\]Správně
Špatně
Nejdříve musíme transponovat matici B – vyměníme řádky za sloupce. Ověříme, jestli se matice mohou vynásobit a násobíme. U matic násobíme řádek sloupcem a jednotlivé členy mezi sebou sčítáme.
-
Otázka 2 / 11
2. Otázka
Urči, jestli existuje součin matic. Pokud ano, zapiš její hodnost
A) \((2;4) \cdot (4;4)^2\)
B) \([(3;4)^T \cdot (3;2)]\cdot (2;1)\)
C) \([(3;3)^2\cdot (2;3)^T]\cdot (4;2)\)
D) \((3;2)\cdot [(3;2)^2-(2;3)]\)
E) \((2;3)\cdot [(3;4)+2\cdot(3;4)]\cdot (3;1)\)
- Pokud součin matic neexistuje, zapiš do hodnosti nuly. A) (ano), hodnost je ( (2); (4)) B) (ano), hodnost je ( (4); (1)) C) (ne), hodnost je ( (0); (0)) D) (ne), hodnost je ( (0); (0)) E) (ne), hodnost je( (0); (0))
Správně
Špatně
Musíme postupovat stejně, jakobychom počítali klasické výpočty, tj. od vnitřních závorek po vnější. Víme, že matice můžeme násobit pouze tehdy, pokud má první matice stejný počet sloupců jako je počet řádků druhé matice. Taky musíme dát pozor na pořadí – u součinu matic nemůžeme zaměňovat.
Nápověda
Zapisuj pouze ano/ne. Do hodnosti vypiš jen čísla, pokud součin neexistuje, zapiš nuly.
-
Otázka 3 / 11
3. Otázka
Vypočítej matici X jako součin matic A,B.
Vypočítej matici Y jako součin matic B,A.
\[
A= \begin{pmatrix}
4 & 0 & 2&1\\
3 & -1 & 0&2 \\
2 & -2 &-1&1\\
1&3&-2&1
\end{pmatrix}\qquad B=\begin{pmatrix}
2 & 3 & 1&0\\
-1 & 1 & 0&1 \\
-2 & 1 &2&3\\
4&0&1&-1
\end{pmatrix}
\]- matice X bude mít prvky (8) (14) (7) (5) (15) (8) (5) (-3) (12) (3) (1) (-6) (7) (4) (-2) (-4) matice Y bude mít prvky (19) (-5) (3) (9) (0) (2) (-4) (2) (2) (4) (-12) (5) (17) (-5) (9) (4)
Správně
Špatně
Musíme dodržet pořadí výpočtu. U matic totiž neplatí komutativní zákon – nedostaneme stejný výsledek při násobení AB a BA.
Matice násobíme řádek krát sloupec a jednotlivé členy mezi sebou sčítáme. Vznikají nám prvky výsledné matice.Nápověda
Na volná políčka vypisujte pouze prvky matice. V případě kladného čísla nepište znaménko +, u záporu mínus pište.
-
Otázka 4 / 11
4. Otázka
Vypočítej
\( (A\cdot B)^T\), jsou-li matice
\[
A= \begin{pmatrix}
1 & 0 & 3\\
-1 & -2 & 1 \\
4 & 1 & -2
\end{pmatrix}\qquad B= \begin{pmatrix}
3 & 0 & 1&-2\\
-1 & 2 & 1&0 \\
3 &- 2 & -1&1
\end{pmatrix}
\]Správně
Špatně
Matice nejdříve vynásobíme. Násobíme řádek první matice sloupcem druhé matice a jednotlivé členy mezi sebou sčítáme. Takto mezi sebou vynásobíme všechny řádky všemi sloupci.
Abychom měli matici transponovanou, vyměníme řádky původní matice za sloupce nové matice a máme výsledek. -
Otázka 5 / 11
5. Otázka
Vypočítej
\(A^T\cdot B-3\cdot B^T\), jsou-li matice
\[
A=\begin{pmatrix}
3 & 1 &2\\
-1 & 0 & -2 \\
3 &2 &-1
\end{pmatrix}\qquad B=
\begin{pmatrix}
-1 & 4 &2\\
1 & 2 & 3 \\
1 &-1 &1
\end{pmatrix}
\]Správně
Špatně
Nejdříve si napíšeme transponovanou matici A, tu potom vynásobíme maticí B. Matici B transponujeme, vynásobíme trojkou a tuto odečteme od součinu výše spočítaného.
-
Otázka 6 / 11
6. Otázka
Vypočítej
\((X+Y)^2\), jsou-li matice
\[
X=\begin{pmatrix}
3 & 2\\
-1 &4
\end{pmatrix}\qquad Y=
\begin{pmatrix}
2 &-3\\
1 &3
\end{pmatrix}
\]Správně
Špatně
Matice nejdříve sečteme. Výslednou matici máme umocnit na druhou mocninu. Víme ale, že matice nejdou umocnit jen tak. Musíme je mezi sebou vynásobit.
-
Otázka 7 / 11
7. Otázka
Vypočítej
\((2U-3V)^2\), jsou-li matice
\[
U=\begin{pmatrix}
1 &-2\\
-2 & 1
\end{pmatrix}\qquad V=
\begin{pmatrix}
-1 &2\\
3 & -2
\end{pmatrix}
\]Správně
Špatně
Nejdříve vynásobíme jednotlivé matice zadanými čísly. Tyto matice poté mezi sebou odečteme a umocníme. Matici umocníme tak, že ji vynásobíme samu sebou.
-
Otázka 8 / 11
8. Otázka
Vypočítej
\((2A+B)^T\cdot C\), jsou-li matice
\[
A=\begin{pmatrix}
1 &3&2\\
-2 & 1&-1
\end{pmatrix}\qquad B=
\begin{pmatrix}
4 &-3&1\\
8 & 1&6
\end{pmatrix}\qquad C=
\begin{pmatrix}
3 &-1&4&0\\
-1 &2&1&2
\end{pmatrix}
\]Správně
Špatně
Spočítáme hodnotu závorky. Postupujeme podle toho, co má přednost. Nejdříve tedy vynásobíme číslem, matice potom sečteme a matici transponujeme, tj. přehodíme řádky za sloupce. Vzniklou matici vynásobíme zadanou maticí a dostaneme výsledek.
-
Otázka 9 / 11
9. Otázka
Vypočítej
\((A+2B)^2\cdot C\), jsou-li matice
\[
A=\begin{pmatrix}
-3 &-2\\
2 & 1
\end{pmatrix}\qquad B=\begin{pmatrix}
2 &1\\
-1 &2
\end{pmatrix}\qquad C=
\begin{pmatrix}
4 &1&-1\\
2 & -1&3
\end{pmatrix}
\]Správně
Špatně
Nejdříve spočítáme hodnotu závorky, poté teprve umocníme. Matici umocňujeme tak, že vynásobíme matici samu sebou. Následně výslednou matici vynásobíme maticí C.
-
Otázka 10 / 11
10. Otázka
Vypočítej
\(A^T\cdot B^T-3(A-B)\), jsou-li matice
\[
A=\begin{pmatrix}
1 &0&0\\
0 & 1&0\\
0&0&1
\end{pmatrix}\qquad B=
\begin{pmatrix}
2 &-1&1\\
1 & 2&3\\
2&-2&1
\end{pmatrix}
\]Správně
Špatně
Nejdříve matice A a B transponujeme. Tyto mezi sebou vynásobíme. Vypočítáme hodnotu závorky, vynásobíme číslem 3 a odečteme od součinu transponovaných matic.
-
Otázka 11 / 11
11. Otázka
Vypočítej
\(X^2-Y^3+2Z^2\), jsou-li matice
\[
X=\begin{pmatrix}
1 &0\\
0 & -1
\end{pmatrix}\qquad Y=
\begin{pmatrix}
1 &0\\
-1 & 1
\end{pmatrix}\qquad Z=\begin{pmatrix}
3 &2\\
1 & 4
\end{pmatrix}
\]Správně
Špatně
Nejdříve umocníme matice. Umocňujeme tak, že násobíme danou matici samu sebou. Takto postupujeme u matic X a Z. U matice Y postupujeme tak, že vynásobíme matici samu sebou a výsledek vynásobíme znovu maticí Y. Matice odečteme/sečteme a máme výsledek.
Algebraické vzorce
Procvičíte si výpočty pomocí algebraických vzorců – 15 příkladů
Algebraické vzorce
Závěrečný přehled
Zodpovězeno 0 z 15 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
Information
Procvičíte si výpočty pomocí algebraických vzorců – 15 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 15 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 15
1. Otázka
Vypočítej
\((3x-6y)^2\)Správně
Špatně
V závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a-b)^2 = a^2-2ab+b^2\).
-
Otázka 2 / 15
2. Otázka
Vypočítej
\((2c-4d)\cdot(2c+4d)\)Správně
Špatně
Závorky jsou téměř stejné. Mají jen rozdílná znaménka. Můžeme použít vzorec \(a^2-b^2=(a+b)(a-b)\). Pokud si náhodou na vzorec nevzpomeneme, musíme násobit každý člen každým.
-
Otázka 3 / 15
3. Otázka
Vypočítej
\(3a-(a+4)^2\)Správně
Špatně
V závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a+b)^2 = a^2+2ab+b^2\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve aplikovat mínusko. Mínus před závorkou mění znaménka v závorce.
-
Otázka 4 / 15
4. Otázka
Rozlož na součin
\(4s^2-16t^2\)Správně
Špatně
Rozlož na součin znamená, že výsledek má být ve tvaru součinu, tj. něco krát něco. Můžeme nejdříve vytknout. Potom vidíme, že jednotlivé členy umíme odmocnit. Zkontrolujeme ještě znaménko – musí být mínus. Použijeme vzorec \(a^2-b^2 =(a-b)(a+b)\).
-
Otázka 5 / 15
5. Otázka
Vypočítej
\((2a+4b)^2-(a-4)^2\)Správně
Špatně
V závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a\pm b)^2 = a^2\pm 2ab+b^2\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve aplikovat mínusko. Mínus před závorkou mění znaménka v závorce. Jednotlivé členy už stačí jen sečíst/odečíst.
-
Otázka 6 / 15
6. Otázka
Vypočítej
\(\dfrac{2}{3}\cdot(x+2y)^2+(\dfrac{1}{3}y-\dfrac{1}{2}x)^2\)Správně
Špatně
V závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a\pm b)^2 = a^2\pm 2ab+b^2\). První závorku ještě po použití vzorce přenásobíme zlomkem. Sečteme/odečteme jednotlivé členy, které mají stejné neznámé a dostaneme výsledek.
-
Otázka 7 / 15
7. Otázka
Rozlož na součin
\(x^8-64y^4\)Správně
Špatně
Rozlož na součin znamená, že výsledek má být ve tvaru součinu, tj. něco krát něco. Vidíme, že jednotlivé členy umíme odmocnit. Zkontrolujeme ještě znaménko – musí být mínus. Použijeme vzorec \(a^2-b^2 =(a-b)(a+b)\).
-
Otázka 8 / 15
8. Otázka
Rozlož na součin
\(16u^4-v^4\)Správně
Špatně
Rozlož na součin znamená, že výsledek má být ve tvaru součinu, tj. něco krát něco. Vidíme, že jednotlivé členy umíme odmocnit. Zkontrolujeme ještě znaménko – musí být mínus. Použijeme vzorec \(a^2-b^2 =(a-b)(a+b)\). Vzorec jde použít dvakrát, protože po prvním rozložení jdou členem znovu umocnit a v jedného ze závorek máme znaménko mínus.
-
Otázka 9 / 15
9. Otázka
Rozlož na součin
\(-8y^2z^2+12yz^3-18z^4\)Správně
Špatně
Rozlož na součin znamená, že výsledek má být ve tvaru součinu, tj. něco krát něco. Můžeme nejdříve vytknout. Vytkneme i znaménko mínus. Potom vidíme, že první a poslední člen umíme odmocnit. Použijeme vzorec \((a-b)^2 =a^2-2ab+b^2\). Zkontrolujeme prostřední člen.
-
Otázka 10 / 15
10. Otázka
Vypočítej
\(\left(x-\dfrac{1}{4}\right)\cdot \left(\dfrac{3}{2}x+4\right)-4\cdot\left(\dfrac{1}{3}-\dfrac{5}{4}x\right)^2\)Správně
Špatně
První závorky musíme roznásobit, tzn. každý člen jedné závorky se vynásobí s každým členem druhé závorky. V další závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a-b)^2 = a^2-2ab+b^2\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve vynásobit členem před závorkou. Nakonec dáme dohramady členy se stejnou neznámou a exponente, spočítáme výsledek.
-
Otázka 11 / 15
11. Otázka
Vypočítej
\(\left(\dfrac{2}{3}a-2\right)^2- \left(\dfrac{1}{2}-\dfrac{3}{2}a\right)^2\)Správně
Špatně
-
Otázka 12 / 15
12. Otázka
Vypočítej
\((7x-2y)^2+(2x-3y)(2x+3y)-(3y-2x)^2\)Správně
Špatně
V závorce nemůžeme nic sečíst/odečíst, musíme použít vzorec \((a-b)^2 = a^2-2ab+b^2\). Při násobení závorky závorkou můžeme použít vzorec \(a^2-b^2 =(a-b)(a+b)\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve aplikovat mínusko. Mínus před závorkou mění znaménka v závorce.
-
Otázka 13 / 15
13. Otázka
Vypočítej
\((x+\sqrt{100-36})(2x-\sqrt{16+9}-x)-3(4-x)(x+4)\)Správně
Špatně
Nejdříve odstraníme odmocninu. Pod odmocninou je +/-, musíme nejdřív spočítat hodnotu a poté teprve odmocnit. Závorky mezi sebou vynásobíme a můžeme si všimnout, že druhé dvě závorky jsou až na znaménko stejné. Použijeme vzorec \(a^2-b^2 =(a-b)(a+b)\). Jednotlivé členy sečteme/odečteme a máme hotovo.
-
Otázka 14 / 15
14. Otázka
Vypočítej
\((n\cdot n+4)^2-(n-\dfrac{1-n}{2})^2\)Správně
Špatně
Nejdříve upravíme členy v závorkách. V druhé závorce potřebujeme dostat jeden zlomek. Upravíme a umocníme čitetele zvlášť a jmenovatele. Využíváme vzorec \((a\pm b)^2 = a^2\pm 2ab+b^2\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve aplikovat mínusko. Mínus před závorkou mění znaménka v závorce. Členy dáme dohromady a máme výsledek.
-
Otázka 15 / 15
15. Otázka
Vypočítej
\((x-4y)^2-3(x+3y-2x)-(2x-y)(2x+y)\)Správně
Špatně
Zkontrolujeme závorky, pokud nejde nic sečíst/odečíst, musíme použít vzorec \((a-b)^2 = a^2-2ab+b^2\) a \(a^2-b^2 =(a-b)(a+b)\). Dáváme pozor na znaménko mínus před závorkou. Je lepší nejdříve spočítat závorku a poté teprve aplikovat mínusko. Mínus před závorkou mění znaménka v závorce.
Příklady - FB 1
Procvič si jednoduché výpočty.
Příklady - FB 1
Závěrečný přehled
Zodpovězeno 0 z 6 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
Information
Procvič si jednoduché výpočty.
Soutěžíme o kredit 10 Kč, který bude připsán na Tvůj uživatelský účet (při registraci získáš navíc ještě další kredit zdarma) a můžeš ho využít k zobrazení řešení vybraných příkladů.
Každá otázka má pouze jednu správnou odpověď. „Test“ je možné vyplnit pouze jedenkrát.
Nezapomeň na konci uvést svůj mail, ať tě máme v případě výhry kde kontaktovat.
Vyhrává ten, kdo:
– má nejvíc bodů (každá správná odpověď je za 1 bod – max. 5 bodů)
– v případě stejného počtu bodů se porovná čas zpracování „testu“
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 6 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 6
1. Otázka
Čtyři hlávky zelí váží celkem 8,4 kilogramů. Dva svazky mrkve váží 850 gramů. Pět svazků mrkve je lehčí než hlávka zelí?
Správně
Špatně
Jedna hlávka váží 2,1 kg, jeden svazek váží 425 g = 0,425 kg.
Pět svazků váží 2,125 kg a to je víc než jedna hlávka zelí. -
Otázka 2 / 6
2. Otázka
Doplň
6 hod + ____ s = 385 min
Správně
Špatně
6 hod = 360 min, 385 – 360 = 25 min krát 60 = 1 500 s
-
Otázka 3 / 6
3. Otázka
Vypočítej
\([100-(25+3\cdot 75)]:(-25) \)
Správně
Špatně
Přednost má násobení, kulatá závorka, hranatá závorka a potom až dělení. Mínus dělím mínusem, získávám kladný výsledek.
-
Otázka 4 / 6
4. Otázka
Vypočítej
\(2^2-\sqrt{169}+(12^2:8)^2\)
Správně
Špatně
Můžeme zároveň umocnit a odmocnit čísla. Dále má přednost závorka, kde nejdříve umocníme a potom až dělíme. Výsledek dáme na druhou mocninu a teprve čísla sčítáme a odčítáme.
-
Otázka 5 / 6
5. Otázka
Vypočítej a výsledek uveď v základním tvaru
\(\dfrac{3}{4}-\dfrac{12}{5}\cdot\dfrac{125}{48}\)
Správně
Špatně
Přednost má násobení. Zlomky můžeme při násobení krátit do kříže nebo pod sebou. Potom teprve odčítáme. Při odčítání hledáme společný jmenovatel. Výsledek má být v základním tvaru, tzn. krátíme dokud jde.
-
Otázka 6 / 6
6. Otázka
Pokud nejsi přihlášená/ý na stránkách, napiš své jméno a mail, abychom Tě mohli v případě výhry kontaktovat.
Správně
Špatně
Je to v pořádku.
Malá násobilka II.
Procvičení malé násobilky – násobení/dělení – 20 příkladů
Malá násobilka II.
Závěrečný přehled
Zodpovězeno 0 z 20 otázek
Otázky:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Procvičení malé násobilky – násobení/dělení – 20 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 20 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 20
1. Otázka
\(4\cdot 7\)
Správně
Špatně
-
Otázka 2 / 20
2. Otázka
\(8\cdot9\)
Správně
Špatně
-
Otázka 3 / 20
3. Otázka
\(6 \cdot8\)
Správně
Špatně
-
Otázka 4 / 20
4. Otázka
\(0\cdot 4\)
Správně
Špatně
-
Otázka 5 / 20
5. Otázka
\(9\cdot 3\)
Správně
Špatně
-
Otázka 6 / 20
6. Otázka
\(8\cdot 5\)
Správně
Špatně
-
Otázka 7 / 20
7. Otázka
\(8\cdot 7\)
Správně
Špatně
-
Otázka 8 / 20
8. Otázka
\(6\cdot 9\)
Správně
Špatně
-
Otázka 9 / 20
9. Otázka
\(10\cdot 10\)
Správně
Špatně
-
Otázka 10 / 20
10. Otázka
\(81:9\)
Správně
Špatně
-
Otázka 11 / 20
11. Otázka
\(70:7\)
Správně
Špatně
-
Otázka 12 / 20
12. Otázka
\(0:5\)
Správně
Špatně
-
Otázka 13 / 20
13. Otázka
\(42:6\)
Správně
Špatně
-
Otázka 14 / 20
14. Otázka
\(25:5\)
Správně
Špatně
-
Otázka 15 / 20
15. Otázka
\(63:9\)
Správně
Špatně
-
Otázka 16 / 20
16. Otázka
\(9:3\)
Správně
Špatně
-
Otázka 17 / 20
17. Otázka
\(12:6\)
Správně
Špatně
-
Otázka 18 / 20
18. Otázka
\(32:4\)
Správně
Špatně
-
Otázka 19 / 20
19. Otázka
\(18:2\)
Správně
Špatně
-
Otázka 20 / 20
20. Otázka
\(3\cdot 5\)
Správně
Špatně
Úpravy lomených výrazů
Procvičení podmínek, úprav a krácení lomených výrazů – 15 příkladů
Úpravy lomených výrazů
Závěrečný přehled
Zodpovězeno 0 z 4 otázek
Otázky:
- 1
- 2
- 3
- 4
Information
Procvičení podmínek, úprav a krácení lomených výrazů – 15 příkladů
Je nám líto, tento kvíz smíte vyplnit pouze jednou.
Quiz is loading…
Pro spuštění procvičování se musíte přihlásit nebo zaregistrovat.
Abyste mohli vyplnit tento kvíz, nejdřív musíte splnit tenhle:
Výsledek
Odpověděli jste správně na 0 z 4 otázek
Váš čas:
Čas vypršel
Získali jste 0 z 0 bodů, (0)
| Průměrný výsledek |
|
| Váš výsledek |
|
Rubriky
- Žádná rubrika 0%
| Umístění | Jméno | Vloženo dne | Body | Výsledek |
|---|---|---|---|---|
| Tabulka se načítá | ||||
| Žádná data | ||||
- 1
- 2
- 3
- 4
- Zodpovězeno
- Poznačené otázky
-
Otázka 1 / 4
1. Otázka
Urči podmínky lomeného výrazu
\(\dfrac{36-m²}{25mn³}\)Správně
Špatně
\(m\cdot n^3\neq 0⇒m\neq 0\:∧\: n^3\neq0\)
Nula na cokoliv je stále nula, proto mocnina nehraje v podmínce žádnou roli. -
Otázka 2 / 4
2. Otázka
Urči podmínky lomeného výrazu
\(\dfrac{4u-4}{5v+5}\)Správně
Špatně
\(\)
\begin{eqnarray*}5v+5v&\neq &0\\
5v&\neq&-5\:/:5\\
v&\neq&-1\end{eqnarray*} -
Otázka 3 / 4
3. Otázka
Urči podmínky lomeného výrazu
\(\dfrac{x-4}{x^2+8x+16}\)Správně
Špatně
Pomocí algebraického vzorce \((a+b)^2=a^2+2ab+b^2\:\:\) upravíme jmenovatel.
\begin{eqnarray*}x^2+8x+16&\neq &0\\
(x+4)^2&\neq&0\\
x+4&\neq&0\\
x&\neq&-4\end{eqnarray*} -
Otázka 4 / 4
4. Otázka
Urči podmínky lomeného výrazu
\(\dfrac{3rs^2+6rs}{6r^2s-3rs}\)Správně
Špatně
Ve jmenovateli vytkneme a dostaneme \(3rs(2r-1)\:\:\) a víme, že se tento součin nesmí rovnat nule. Proto určíme pro každý člen podmínku zvlášť, tj. pro r, s a pro celou závorku.