
Přímá/nepřímá úměra, procenta
Úměra a procenta řešené trojčlenkou …
100 Kč
Popis
V online kurzu se naučíte ze slovního zadání rozeznat, jestli se jedná o přímou nebo nepřímou úměru. Dále sestavit a následně spočítat trojčlenku. Trojčlenka se využívá i při počítání s procenty.
Kurz obsahuje 3 písemně komentované příklady krok po kroku, 10 příkladů vyřešených a 15 příkladů k procvičení.
Procenta se objevují v každém přijímačkovém testu.
Online kurz máte k dispozici po dobu jednoho měsíce.
Najdete zde např.:
1) Při denní spotřebě 0,6 t uhlí vystačí jeho zásoba na 72 dny. Na kolik dní vystačí tatáž zásoba, jestliže bude denní spotřeba jen 540 kg uhlí?
2) Elektrické vedení je dlouhé 6,2 km a na prohnutí drátů je potřeba přidat 3,4 % délky. Kolik metrů drátu montéři potřebují, jestliže má vedení osm drátů?
3) Kniha byla z 320 Kč zdražena o 15 %. Protože nešla na odbyt, zlevnil ji knihkupec o 10 %. Kolik byla její koncová cena? Kolik % z původní ceny činí tato cena?
Ukázka z kurzu
Zadání
Pět dlaždičů by vydláždilo náměstí za 12 dní. Za kolik dní by toto náměstí vydláždili 4 dlaždiči?
Řešení
Závislé veličiny, se kterými budeme pracovat, jsou počet dělníků a počet dní. Sestavíme si schéma.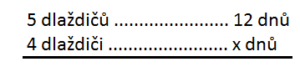
Potřebujeme zapsat šipky. Musíme si ujasnit, jestli se jedná o přímou nebo nepřímou úměru.
Zeptáme se: čím míň dělníků, tím míň času nebo tím více času budou potřebovat? Správně je: tím více času. Máme tedy nepřímou úměru, tzn. že šipky nám jdou proti sobě. Šipku vpravo začínáme opět od neznámé.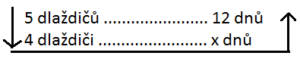
Abychom spočítali výsledek, musíme sestavit rovnici. Postupujeme opět podle šipek.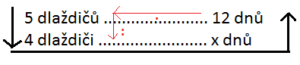
Dopočet příkladu a spoustu dalších najdete v kurzu Přímá/nepřímá úměra, procenta.

