Obvody a obsahy obrazců, Pythagorova věta
Výpočty klasických i netradičních obrazců …
100 Kč
Popis
V online kurzu si zopakujete výpočty základních geometrických útvarů – čtverec, obdélník, kruh, trojúhelník, lichoběžník. V kurzu najdete různě seskládané obrazce pospolu a naučíte se vyřešit i zdánlivě zapeklité tvary.
Pythagorova věta vás bude provázet po celou dobu studia nejen na střední ale i vysoké škole. Proto čím dříve se ji naučíte používat, tím lépe pro vaše další studium.
Kurz obsahuje 3 písemně komentované příklady krok po kroku, 10 příkladů vyřešených a\(\nobreakspace\)10\(\nobreakspace\)příkladů k procvičení.
Online kurz máte k dispozici po dobu jednoho měsíce.
Najdete zde např.:
1) Urči obsah vybarvené části obrazce.
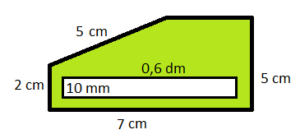2) Vypočítej délku cyklistické trasy.
Ukázka z kurzu
Pythagorova věta
$$c^{2}=a^{2}+b^{2}$$
Součet druhých mocnin odvěsen se rovná druhé mocnině přepony. Písmena značíme podle stran, proto dávejte pozor, jestli bude trojúhelník označen jinými písmeny. c nám značí přeponu (nejdelší strana trojúhelníku, vždy naproti pravého úhlu), a a b značí odvěsny.
Příklad
Obsah lichoběžníku je \(35\:m^{2}\) a jeho výška je 5 m. Základna trojúhelníku je o 2 m delší než spodní základna lichoběžníku. Domeček je vysoký 8 m. Obvod jednoho okna je \(4\pi\:m\). Obsah dveří je \(200\:dm^{2}\). Vypočítej součet obsahů vybarvených částí domečku.
Řešení
Domeček si rozdělíme na lichoběžník a trojúhelník.
lichoběžník:
– obsah je \(35\:m^{2}\)
– výška je 5 m
– delší základna = základna trojúhelníku, tj. o 2 m delší než kratší základna a ⇒ c = a + 2
\begin{eqnarray*}S_{l}&= &\dfrac{(a+c) \cdot v}{2}\\[2ex]
35&= &\dfrac{(a+a+2)\cdot 5}{2}\\[2ex]
35&= &\dfrac{(2a+2)\cdot 5}{2}\:/\cdot2\\[2ex]
2\cdot 35&= &(2a+2)\cdot 5\:/:5\\[2ex]
\dfrac{70}{5}&= &2(a+1)\\[2ex]
14&= &2(a+1)\:/:2\\
7&= &a+1\\
7-1&= &a\\
a&= &6\: m \Rightarrow c=a+2=6+2=8\end{eqnarray*}
Dokončení příkladu a další zajímavé obrazce najdete v placené verzi.
